Back to: Mathematics Primary 5
HELLO, WELCOME BACK TO CLASS
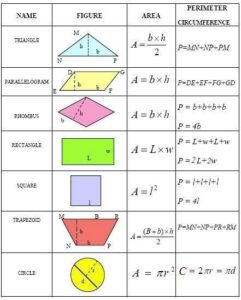
Perimeter simply means addition of all the sides of a given plane shape. Plane shapes can be classified into two types:
- Regular shapes.
- Irregular shapes.
PERIMETERS OF REGULAR PLANE SHAPES
The regular plane shapes are as follows:
- Square
- Rectangle
- Triangle
- Circle
- Kite
- Trapezium
- Rhombus
- Parallelogram
Example 1
Find the perimeter of the rectangle below:
|
Solution
Perimeter = sum of all sides OR 2L + 2B
The shape has four sides. 2(7) + 2(5)
Perimeter = 7 + 7 + 5 + 5 14 + 10
Perimeter = 24cm 24cm
Example 2
Find the perimeter of the square below:
|
Solution
A square has four sides that are all equal
Perimeter = sum of all sides OR 4 Lenght
Perimeter = 5 + 5 + 5 + 5 4 5
Perimeters = 20cm 20cm
Example 3
Find the perimeter of the shape below:
Solution
The shape (a trapezium) has four sides.
Perimeter = sum of all sides
Perimeter = 80 + 50 + 100 + 110
Perimeter = 340m
PERIMETER OF IRREGULAR PLANE SHAPES
Example 1. Find the perimeter of the shape below:
Solution
The shape has 5 sides.
Perimeter = sum of all sides
Perimeter = 5 + 4 + 4 + 4 + 3
Perimeter = 20in
Example 2. Find the perimeter of the shape below:
Solution
The shape has six sides. First find the missing sides
There are 3 missing sides, the first one is 5m, the second one is 7m and the third one is ( 5 + 11 = 16m )
Perimeters = (7 +5) + 5 + 5 + 11 + 7 + 16
Perimeters = 56m
Circumference of a Circle
The distance around a rectangle or a square is as you might remember called the perimeter. The distance around a circle on the other hand is called the circumference (c). Circumference of the circle or perimeter of the circle is the measurement of the boundary of the circle. Whereas the area of a circle defines the region occupied by it.
A line that is drawn straight through the midpoint of a circle and that has its end points on the circle border is called the diameter (d)
Half of the diameter, or the distance from the midpoint to the circle border, is called the radius of the circle (r).
The circumference of a circle is found using this formula:
Circumference (or) perimeter of a circle = 2πR or C=π⋅d where,
R is the radius of the circle
π is the mathematical constant with an approximate (up to two decimal points) value of 3.14
Pi (π) is a special mathematical constant; it is the ratio of circumference to diameter of any circle.
where C = π D
C is the circumference of the circle
D is the diameter of the circle
For example: If the radius of the circle is 4cm then find its circumference.
Given: Radius = 4cm
Circumference = 2πr
= 2 x 3.14 x 4
= 25.12 cm
Examples
Question 1: What is the circumference of the circle with diameter 4 cm?
Solution:
Since the diameter is known to us, we can calculate the radius of the circle,
Therefore, Circumference of the Circle = 2 x 3.14 x 2 = 12.56 cm.
Question 2: Find the radius of the circle having C = 50 cm.
Solution:
Circumference = 50 cm
As per formula, C = 2 π r
This implies, 50 = 2 π r
50/2 = 2 π r/2
25 = π r
or r = 25/π
Therefore, the radius of the circle is 25/π cm.
AREAS OF PLANE SHAPES
Area is measured in square units. The area of regular plane shapes is given in the table below;
Examples: find the area of the rectangle below:
Solution
Area of rectangle = length bredth
Area of rectangle = 9 4
Area of rectangle = 36m2
Example 2: find the area of the shape below:
Solution
The shape above is a trapezium.
Area of a trapezium =
Area of trapezium = (6 + 8) 4
Area of trapezium = 14 4
Area of trapezium =
Area of trapezium =
Area of trapezium = 28
Example 3: find the area of the shape below:
Solution
The shape is a square.
Area of a square = length length
Area of square = 8 8
Area of square = 64cm2
Examples 4: find the area of the shape below:
Solution
The shape is a circle. = 3.14 or 22/7
Area of a circle =
Area of circle = 3.14 2 2
Area of circle = 12.56cm2
Example 5: find the area of the shape below:
Solution
The shape is a triangle.
Area of a triangle = base of triangle height of triangle
Area of triangle = 11 10
Area of triangle =
Area of triangle =
Area of triangle = 55cm2
AREA OF IRREGULAR PLANE SHAPES
When finding the areas of irregular plane shapes, split the irregular plane shape in regular plane shapes. Find their areas and sum them all together.
Example: find the area of the shape below:
Solution
The shape can be split into two regular plane shapes A and B
A = a rectangle with length 8m and breadth 4m
B = a square with length 10m
Area of A = 8 4
Area of A = 32m2
Area of B = 10 10
Area of B = 100m2
Area of the irregular plane shape = 32 + 100
Area of the irregular plane shape = 132m2
AREA OF SHADED PORTIONS
Example: find the area of the shaded portion in the figure below:
Solution
The shaded portion is between a rectangle (the bigger shape) and a square (the smaller shape)
Area of the rectangle = length breadth
Area of rectangle = 20
Area of rectangle = 300cm2
Area of the square = length length
Area of square = 8 8
Area of square = 64cm2
Area of shaded portion = area of rectangle – area of square
Area of shaded portion = 300 – 64
Area of shaded portion = 236cm2
Area of Complex figures
A complex figure is made up of two or more shapes. To find the area of a complex figure, break the figure into smaller parts.
Example 6: Find the area of the swimming pool at Dew’s hotel.
Solution:
Step 1: Break up the figure into smaller parts. Look for rectangles and squares.
Step 2: Find the area of each part.
Square
Area = side x side
A = 10m x 10m
A = 100 square meters.
Rectangles
A = length x width
A = 12m x 6m
A = 72 square meters
Step 3: Add the areas.
The area is 72 + 100 = 172 square meters.
Quiz
- Find the perimeter of the following shapes:
