ADDITION AND SUBTRACTION OF FRACTION

Back to: Mathematics Primary 4

HELLO, WELCOME BACK TO CLASS

 

To add or subtract fractions, they must be converted into fractions that have a common denominator. A common denominator is a number that is evenly divisible by the denominators of all of the original fraction. (That is, the denominators of the original fractions are all factors of the common denominator). After finding a suitable common denominator, each of the fractions must be converted into a fraction that has this common denominator. To do so, multiply the numerator and denominator of each of the fractions by the same integer, so that the number obtained in the denominator will be the number that was chosen to be the common denominator. Multiplying the numerator and denominator by the same number is the same as multiplying by 1, and its value remains unchanged. Once the fractions have a common denominator, add or subtract the new numerators and reduce the resulting fractions to lowest terms where possible.

Adding Fractions with Unlike Denominators

To add fractions with unlike denominators, first rewrite them with like denominator.

Then, you know what to do! The steps are shown below.

1. Find a common denominator.
2. Rewrite each fraction using the common denominator.
3. Now that the fractions have a common denominator, you can add the numerators.
4. Simplify to lowest terms, expressing improper fractions as mixed numbers.

You can always find a common denominator by multiplying the two denominators together. See the example below

F0r example:

Example. 2 3  + 1 4 . Solution.  The lowest common multiple of 3 and 4 is their product, 12. We will convert each fraction to an equivalent fraction with denominator 12. 2 3  + 1 4  =  8  12  +  3  12          = 11 12 .   We converted 2 3  to  8  12   by saying, “3 goes into 12 four times. Four times 2 is 8.” (In that way, we multiplied both 2 and 3 by the same number, namely 4. We converted 1 4  to  3  12   by saying, “4 goes into 12 three times. Three times 1 is 3.”  (We multiplied both 1 and 4 by 3.) The fact that we say what we do shows again that arithmetic is a spoken skill. In practice, it is necessary to write the common denominator only once: 2 3  + 1 4  = 8 + 3 12  = 11 12 .     Example. 4 5  +  2  15 Solution.  The LCM of 5 and 15 is 15.  Therefore, 4 5  +  2  15  = 12  +  2 15  = 14 15 .   We changed 4 5  to 12 15   by saying, “5 goes into 15 three times. Three times 4 is 12.” We did not change  2  15  , because we are not changing the denominator 15.     Example . 2 3  + 1 6  +  7  12 Solution.  The LCM of 3, 6, and 12  is 12.   2 3  + 1 6  +  7  12   = 8 + 2 + 7 12 2 3  + 1 6  +  7 12   = 17 12   2 3  + 1 6  +  7 12   =  1  5  12 . We converted 2 3   to  8  12   by saying, “3 goes into 12 four times. Four times 2 is 8.” We converted 1 6   to  2  12   by saying, “6 goes into 12 two times. Two times 1 is 2.”   We did not change  7  12  , because we are not changing the denominator 12. Finally, we changed the improper fraction 17 12   to  1  5  12   By dividing 17 by 12. “12 goes into 17 one (1) time with remainder 5.”     Example . 5 6  + 7 9 Solution.  The LCM of 6 and 9 is 18.   5 6  + 7 9   = 15 + 14 18   = 29 18   =  1 11 18 . We changed 5 6   to 15 18   by multiplying both terms by 3.   We changed 7 9   to 14 18   by multiplying both terms by 2.     Example .    Add mentally 1 2  + 1 4 .     Answer. 1 2  is how many 1 4 ‘s?   1 2  = 2 4 . Just as 1 is half of 2, so 2 is half of 4.  Therefore, 1 2  + 1 4  = 3 4 . The student should not have to write any problem in which one of   the fractions is 1 2 , and the denominator of the other is even. For example, 1 2  +  2  10  =  7  10     — because 1 2  =  5  10 . Example 8.   In a recent exam, one eighth of the students got A, two fifths got B, and the rest got C.  What fraction got C? Solution.   Let 1 represent the whole number of students.  Then the question is: 1 8  + 2 5  + ?  = 1 . Now, 1 8  + 2 5  = 5 + 16 40  = 21 40 .   The rest, the fraction that got C, is the complement of 21 40 .   It is 19 40 .

4. How do we add mixed numbers?   Add the whole numbers and add the fractions separately.

Example 9.    4 3 8   +  2 2 8   =  6 5 8 .     Example 10.    3 2 5   +  1 4 5   =  4 6 5 .   But 6 5  is improper, we must change it to a mixed number: 46 5  = 1 1 5 . Therefore, 4 6 5   =  4 + 1 1 5   =  5 1 5 . Solution.  When the denominators are different, we may arrange the work vertically; although that is not necessary. To add the fractions, the denominators must be the same.  The LCM of 4 and 8 is 8. We will change 3 4  to 6 8 — by multiplying both terms by 2:   We added  6 + 3 = 9. 6 8  + 5 8  = 11 8  = 1 3 8 .      9 + 1 3 8  = 10 3 8 .

 

Subtraction of Fraction

Example.

8

4 5

− 1

1 5

Solution.  In this example, we may simply subtract the whole numbers and subtract the fractions — similarly to adding mixed numbers.

Example 1.

8

4 5

− 1

1 5

=

7

3 5

.

But consider the following, in which the fractions are reversed:

Example 1.

8

1 5

− 1

4 5

.

 

How can we deal with that?  We cannot take

4 5

from

1 5

.

 

8

1 5

− 1

4 5

.

We need more fifths. Where will we get them?  From 8.  We will

break off 1 from 8, and decompose it into

5 5

.

We will then add those

5 5

with the original

1 5

, making a total of

6 5

.

Then:

“1 from 7 is 6.

4 5

from

6 5

is

2 5

.”

Actually, the simplest way to do this problem is mentally

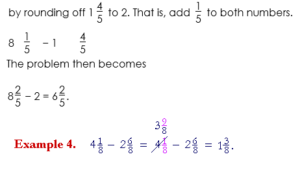
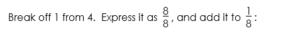
Now the mystery, if any, is:  How does that numerator get to be 9?

9 is the sum of the original numerator 1 and denominator 8:

fraction becomes 4-fourths + 2 -fourths = 6-fourths:

 

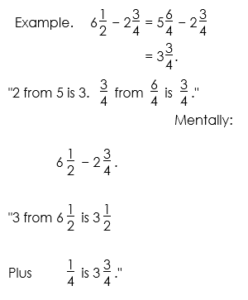
Quiz

1. Rachel rode her bike for one-fifth of a mile on Monday and two-fifths of a mile on Tuesday. How many miles did she ride altogether?
2. Stefanie swam four-fifths of a lap in the morning and seven-fifteenths of a lap in the evening. How much farther did Stefanie swim in the morning than in the evening

For more class notes, homework help, exam practice, download our App HERE

Join ClassNotes.ng Telegram Community for exclusive content and support HERE