Back to: Mathematics Primary 6
HELLO, WELCOME BACK TO CLASS
The lowest or least common multiple of two or more integers is denoted by LCM. The LCM of two numbers is the lowest positive number that is evenly divisible by both numbers. The least common multiple, or LCM, is another number that’s useful in solving many math problems.
The HCF (Highest Common Factor) of two or more than two numbers is the greatest number that divides each of them.
We will discuss here about the method of LCM. (least common multiple).
Let us consider the numbers 8, 12 and 16.
Multiples of 8 are → 8, 16, 24, 32, 40, 48, 56, 64, 72, 80, 88, 96, ……
Multiples of 12 are → 12, 24, 36, 48, 60, 72, 84, 96, 108, 120, 132, ……
Multiples of 16 are → 16, 32, 48, 64, 80, 96, 112, 128, 144, 160, 176, ……
The common multiples of 8, 12, 16 are 48, 96, ……
The least common multiple of 8, 12 and 16 is 48. (Smallest common multiple)
Finding L.C.M.
To find the L.C.M. we find prime factors of the given numbers. Remember, we consider common prime factors only.
Example: Find the L.C.M. of 12, 16 and 24.
First we find the prime factors of the given numbers.
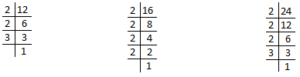
12 = 2 × 2 × 3
16 = 2 × 2 × 2 × 2
24 = 2 × 2 × 2 × 2 × 3
(2 comes maximum 4 times and 3 comes maximum once only.)
Therefore L.C.M. = 2 × 2 × 2 × 2 × 3 = 48 (which is the product of their prime factors.)
We can also find the L.C.M. of the given numbers by dividing all the numbers at the same time by a number that divides at least two of the given numbers.
 |
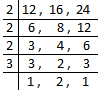1. When a number is not exactly divisible, we write the number itself below the line.
2. When we cannot divide the numbers by a common factor exactly we discontinue dividing the numbers. |
L.C.M. = 2 × 2 × 2 × 3 × 2 = 48
Finding HCF
We will discuss here about the method of h.c.f. (highest common factor).
Let us consider two numbers 16 and 24.
Factor of 16 are → 1, 2, 4, 8, 16
Factor of 24 are → 1, 2, 3, 4, 6, 8, 12,
16 = 1 × 16, or 2 × 8, or 4 × 4
24 = 1 × 24, or 2 × 12, or 3 × 8, or 4 × 6
We see that the highest common factor of 16 and 24 is 8.
Finding H.C.F.
There are three methods of finding H.C.F. of two or more numbers.
- Factorization Method
- Prime Factorization Method
- Division Method
In this lesson we will consider only the second method which is by prime factorization.
H.C.F. by prime factorization method
Let us consider an example. Find the H.C.F. of 24, 36 and 48.
First we find the prime factors of 24, 36 and 48.
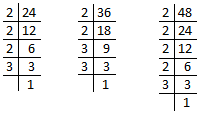
24 = 2 × 2 × 2 × 3
36 = 2 × 2 × 3 × 3
48 = 2 × 2 × 2 × 2 × 3
The common prime factors = 2, 2, 3 H.C.F. = 2 × 2 × 3 = 12
EVALUATION
- Find the L.C.M. of the following by finding common prime factors.
(i) 60, 75, 120
(ii) 48, 80, 112
(iii) 18, 54, 72
(iv) 10, 15, 25
(v) 20, 35, 45
(vi) 16, 24, 48
- Find the H.C.F. of the following by prime factorization method.
(i) 24 and 36
(ii) 56 and 72
(iii) 21 and 35
(iv) 56 and 70
(v) 45 and 81
(vi) 42 and 49
(vii) 44, 66 and 110
(viii) 48, 64 and 120
(ix) 12, 15 and 18
(x) 75 and 125
(xi) 64 and 78
(xii) 27, 36 and 54
School Owner? Looking for ready-made content and tools to save time and grow easily? Book a free demo session now
Get more class notes, videos, homework help, exam practice on Android [DOWNLOAD]
Get more class notes, videos, homework help, exam practice on iPhone [DOWNLOAD]