Back to: MATHEMATICS SS1
Welcome to class!
In today’s class, we will be talking about the circle and its properties. Enjoy the class!
Circle and its Properties
Definition
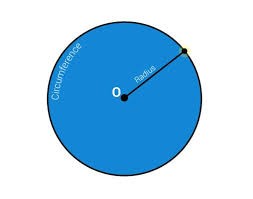
A circle is a collection of points where all the points are equidistant from the given point called the centre “O”. Some of the important terminologies used in the circle are as follows:
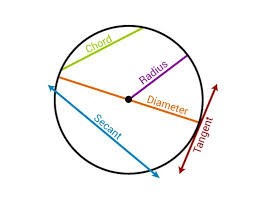
| Terms | Description |
| Circumference | The boundary of the circle is known as the circumference |
| Radius | The line from the centre ”O” of the circle to the circumference of the circle is called the radius and it is denoted by “r” |
| Diameter | The line that passes through the centre of the circle and touches the two points on the circumference is called the diameter and it is denoted by the symbol “D” |
| Arc | Arc is the part of the circumference where the largest arc is called the major arc and the smaller one is called the minor arc |
| Sector | The sector is a slice of a circle bounded by two radii and the included arc of a circle |
| Chord | The straight line that joins any two points in a circle is called a chord |
| Tangent | A line that touches the circumference of a circle at a point is called the tangent |
| Secant | A line that cuts the circle at the two distinct points is known as the secant |
Circle properties
Some of the important properties of the circle are as follows:
- The circles are said to be congruent if they have equal radii
- The diameter of a circle is the longest chord of a circle
- Equal chords and equal circles have an equal circumference
- The radius drawn perpendicular to the chord bisects the chord
- Circles having different radius are similar
- A circle can circumscribe a rectangle, trapezium, triangle, square, kite
- A circle can be inscribed inside a square, triangle and kite
- The chords that are equidistant from the centre are equal in length
- The distance from the centre of the circle to the longest chord (diameter) is zero
- The perpendicular distance from the centre of the circle decreases when the length of the chord increases
- If the tangents are drawn at the end of the diameter, they are parallel to each other
- An isosceles triangle is formed when the radii joining the ends of a chord to the centre of a circle
Circle formulas
Area of a circle, A = πr2 square units
The circumference of a circle = 2πr units
The circumference of a circle formula is also written as πd
Where,
Diameter = 2 x Radius
D = 2r
Here “r” represents the radius of a circle.
Circle problem
The sample example to find the area and circumference of a circle is given below.
Question
Find the area and circumference of a circle having the diameter value of 10 cm?
Solution
Given
Diameter, D = 10 cm
We know that diameter = 2 x Radius
Therefore, radius, r = d/2
r = 10/2 = 5
So, the radius is 5 cm.
Area of a circle, A = πr2 square units
A = 3.14 x 5 x 5
Where,
π = 3.14
A = 3.14 x 25
A = 78.5 cm2
Therefore, the area of a circle is 78.5 square units
The circumference of a circle = 2πr units
C = 2 x 3.14 x 5
C = 10 x 3.14
C = 31. 4 cm
Therefore, the circumference of a circle is 31.4 units.
In our next class, we will be talking about Trigonometric Ratio. We hope you enjoyed the class.
Should you have any further question, feel free to ask in the comment section below and trust us to respond as soon as possible.
Ready to make school management and growth easy? Book your free onboarding session nowGet more class notes, videos, homework help, exam practice on Android [DOWNLOAD]
Get more class notes, videos, homework help, exam practice on iPhone [DOWNLOAD]