Back to: MATHEMATICS SS1
Welcome to class!
In today’s class, we will be talking about the solution of the quadratic equation by graphical method. Enjoy the class!
The solution of Quadratic Equation by Graphical Method
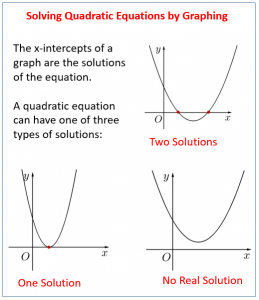
Quadratic equation with two solutions
We will now graph a quadratic equation that has two solutions. The solutions are given by the two points where the graph intersects the x-axis.
Example:
Solve the equation x2 + x – 3 = 0 by drawing its graph for –3 ≤ x ≤ 2.
Solution
Rewrite the quadratic equation x2 + x – 3 = 0 as the quadratic function y = x2 + x – 3
Draw the graph for y = x2 + x – 3 for –3 ≤ x ≤ 2.
| x | –3 | –2 | –1 | 0 | 1 | 2 |
| y | 3 | –1 | –3 | –3 | –1 | 3 |
The solution for the equation x2 + x – 3 can be obtained by looking at the points where the graph y = x2 + x – 3 cuts the x-axis (i.e. y = 0).
The graph y = x2 + x – 3, cuts the x-axis at x 1.3 and x –2.3
So, the solution for the equation x + x –3 is x 1.3 or x –2.3.
Recall that in the quadratic formula, the discriminant b2 – 4ac is positive when there are two distinct real solutions (or roots). How to solve the quadratic equation by graphing?
It uses the vertex formula to get the vertex which also gives an idea of what values to choose to plot the points. This is an example where the coefficient of x2 is positive.
Quadratic equation with one solution
Example:
By plotting the graph, solve the equation 6x – 9 – x2 = 0.
Solution
| x | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
| y | –9 | –4 | –1 | 0 | –1 | –4 | –9 |
Notice that the graph does not cross the x-axis, but touches the x-axis at x = 3. This means that the equation 6x – 9 – x2 = 0 has one solution (or equal roots) of x = 3.
Recall that in the quadratic formula, in such a case where the roots are equal, the discriminant b2 – 4ac = 0.
Quadratic equation with no real solution
Example:
Solve the equation x2 + 4x + 8 = 0 using the graphical method.
Solution
| x | –4 | –3 | –2 | –1 | 0 | 1 |
| y | 8 | 5 | 4 | 5 | 8 | 13 |
Notice that the graph does not cross or touch the x-axis. This means that the equation x2 + 4x + 8 = 0 does not have any real solution (or roots).
In our next class, we will be talking about the Idea of Sets. We hope you enjoyed the class.
Should you have any further question, feel free to ask in the comment section below and trust us to respond as soon as possible.
School Owner? Looking for ready-made content and tools to save time and grow easily? Book a free demo session nowGet more class notes, videos, homework help, exam practice on Android [DOWNLOAD]
Get more class notes, videos, homework help, exam practice on iPhone [DOWNLOAD]
This is great
Makes reading easy