Back to: MATHEMATICS SS1
Welcome to class!
In today’s class, we will be talking about construction: construction of quadrilateral polygon; construction of equilateral triangle; locus of moving points. Enjoy the class!
Construction: Construction of Quadrilateral Polygon; Construction of Equilateral Triangle; Locus of Moving Points
Construction of quadrilateral polygon
| A construction in mathematics is an accurate drawing done usually using only instruments such as a ruler as a straight edge and a pair of compasses.
When drawing a construction, leave all of your construction arcs and lines. |
Construction of quadrilaterals
- Quadrilaterals are four-sided polygons. Types of quadrilaterals include squares, rectangles and parallelograms.
- To be able to construct quadrilaterals, certain information is needed about the sizes of the angles and sides of the shape.
- The instruments used for constructions, which include ruler, compasses and protractors are described.
Some of the types of constructions of quadrilaterals are described below:
| Construct a rectangle with sides of 5 cm and 6 cm. | |
| Step 1: Measure a 5 cm line AB with a ruler.
Step 2: Make a right angle at A. Step 3: Draw an arc, centre A, length 6 cm, mark point C. Step 4: Make a right angle at B. Step 5: Draw an arc, centre B, length 6 cm, mark point D. Step 6: Join C and D |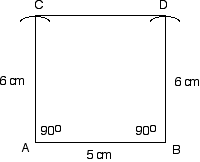
 |
|
Construct a parallelogram PQRS with a base PQ of 6 cm an angle of 60o and the other side of 4 cm. |
|
| Step 1: Measure the base side, PQ, 6 cm long, with a ruler. |
 |
| Step 2: Make an angle of 60o at P. |
 |
| Step 3: Draw an arc, centre P, radius 4 cm, mark point S. |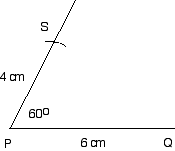
 |
| Step 4: Draw an arc, centre S, radius 6 cm. Draw an arc, centre Q, radius 4 cm. |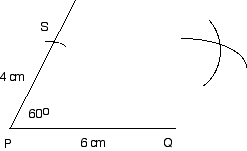
 |
| Step 5: Where the arcs intersect is point R. Join PQRS. |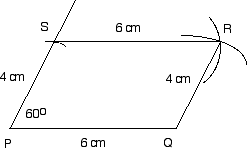
 |
Construction of an equilateral triangle
| Method 1:
Given: the length of one side of the triangle |
 |
Steps:
- Place your compass point on A and measure the distance to point B. Swing an arc of this size above (or below) the segment.
- Without changing the span on the compass, place the compass point on B and swing the same arc, intersecting with the first arc.
- Label the point of intersection as the third vertex of the equilateral triangle.
 |
|
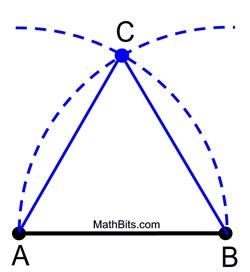Proof of construction:
Circle A is congruent to circle B, since they were each formed using the same radius length, AB. Since AB and AC are lengths of radii of circle A, they are equal. Similarly, AB and BC are radii of circle B and are equal. Therefore, AB = AC = BC by substitution (or transitive property). Since congruent segments have equal lengths, and ΔABC is equilateral (having three congruent sides).
| Method 2
Given: a piece of paper |
|
Steps:
- Place your compass point on the paper and draw a circle. (Keep this compass span!)
- Place a dot, labelled A, anywhere on the circumference of the circle to act as a starting point.
- Without changing the span on the compass, place the compass point on A and swing a small arc crossing the circumference of the circle.
- Without changing the span on the compass, move the compass point to the intersection of the previous arc and the circumference and make another small arc on the circumference of the circle.
- Keep repeating this process of “stepping” around the circle until you return to point A.
- Starting at A, connect every other arc on the circle to form the equilateral triangle.
 |
|
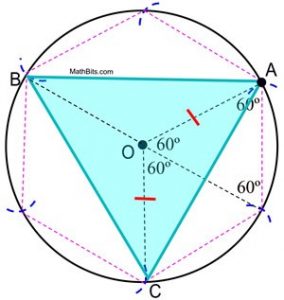Proof of construction:
The proof of the inscribed regular hexagon shows that the central angles of a regular hexagon contain 60º. The central angles of the triangle inscribed in this circle contain 120º. Since ΔAOC is isosceles (OA and OC are radii lengths), m∠OCA = m∠OAC = ½ (180 – 120) = 30º. ΔAOC ΔCOB ΔBOA by SAS. By CPCTC, ∠OCB ∠OCA and m∠OCB = 30º by substitution and m∠BCA = 60º. In similar fashion, we have m∠ACB = m∠CBA = m∠BAC = 60º and equilateral ΔABC.
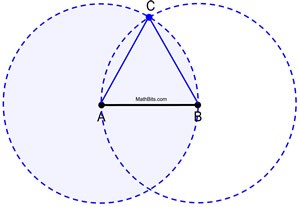
Locus of moving points
When a point moves in a plane according to some given conditions the path along which it moves is called a locus. (Plural of the locus is loci.).
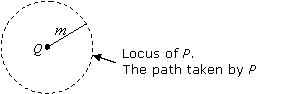
Condition 1:
A point P moves such that it is always m units from the point Q
Locus formed: A circle with centre Q and radius m.
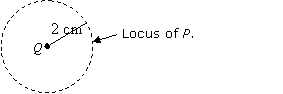
Example:
Construct the locus of a point P at a constant distance of 2 cm from a fixed point Q.
Solution
Construct a circle with centre Q and radius 2 cm.
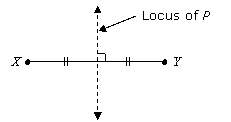
Condition 2:
A point P moves such that it is equidistant from two fixed points X and Y
Locus formed: A perpendicular bisector of the line XY.
Example:
Construct the locus of point P moving equidistant from fixed points X and Y and XY = 6 cm.
Solution
Construct a perpendicular bisector of the line XY.
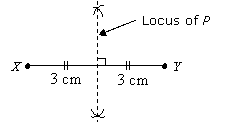
Condition 3:
A point P moves so that it is always m units from a straight-line AB
Locus formed: A pair of parallel lines m units from AB.
Example:
Construct the locus of a point P that moves a constant distant of 2 cm from a straight line AB.
Solution
Construct a pair of parallel lines 2 cm from AB.
Condition 4:
A point P moves so that it is always equidistant from two intersecting lines AB and CD
Locus formed: Angle bisectors of angles between lines AB and CD.
Example:
The following figure shows two straight lines AB and CD intersect at point O. Construct the locus of point P such that it is always equidistant from AB and CD.
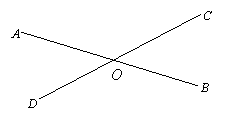
Solution
Construct angles bisectors of angles between lines AB and CD.
In our next class, we will be talking about Deductive Proof: Sum of Angles of a Triangle; Revision of Angles on Parallel Line Cut by a Transversal Line. We hope you enjoyed the class.
Should you have any further question, feel free to ask in the comment section below and trust us to respond as soon as possible.
School Owner? Looking for ready-made content and tools to save time and grow easily? Book a free demo session nowGet more class notes, videos, homework help, exam practice on Android [DOWNLOAD]
Get more class notes, videos, homework help, exam practice on iPhone [DOWNLOAD]