Back to: MATHEMATICS SS1
Welcome to class!
In today’s class, we will be talking about deductive proof: the sum of angles of a triangle; revision of angles on parallel line cut by a transversal line. Enjoy the class!
Deductive Proof: Sum of Angles of a Triangle; Revision of Angles on Parallel Line Cut by a Transversal Line
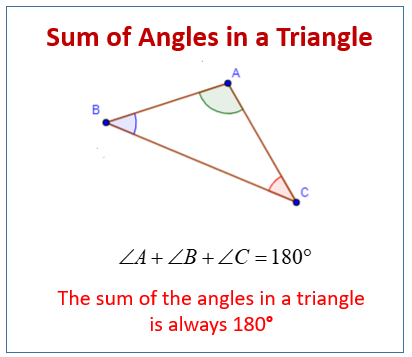
Sum of angles of a triangle
| In a triangle, the three interior angles always add to 180°:
A + B + C = 180° |
Try it yourself (drag the points):
68° + 41° + 71° = 180°
We can use that fact to find a missing angle in a triangle:
Example:
Find the Missing Angle “C”
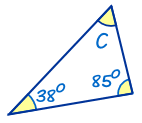
Start With:A + B + C = 180°
Fill in what we know:38° + 85° + C = 180°
Rearrange C = 180° − 38° − 85°
Calculate: C = 57°
Proof
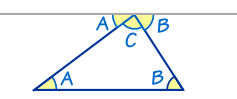
This is proof that the angles in a triangle equal 180°:
The top line (that touches the top of the triangle) is
running parallel to the base of the triangle.
So:
angles A are the same
angles B are the same
And you can easily see that A + C + B does a complete rotation from one side of the straight line to the other, or 180°
Angles on parallel line cut by a transversal line
Two lines that are stretched into infinity and still never intersect are called coplanar lines and are said to be parallel lines. The symbol for “parallel to” is //.
If we have two lines (they don’t have to be parallel) and have a third line that crosses them as in the figure below – the crossing line is called a transversal:
In the following figure:
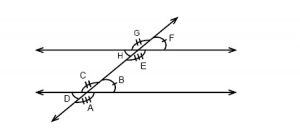
If we draw to parallel lines and then draw a line transversal through them we will get eight different angles.
The eight angles will together form four pairs of corresponding angles. Angles F and B in the figure above constitutes one of the pairs. Corresponding angles are congruent if the two lines are parallel. All angles that have the same position with regards to the parallel lines and the transversal are corresponding pairs.
Angles that are in the area between the parallel lines like angle H and C above are called interior angles whereas the angles that are on the outside of the two parallel lines like D and G are called exterior angles.
Angles that are on the opposite sides of the transversal are called alternate angles e.g. H and B.
Angles that share the same vertex and have a common ray, like angles G and F or C and B in the figure above are called adjacent angles. As in this case where the adjacent angles are formed by two lines intersecting we will get two pairs of adjacent angles (G + F and H + E) that are both supplementary.
Two angles that are opposite each other as D and B in the figure above are called vertical angles. Vertical angles are always congruent.
- ∠A ∠F ∠G ∠D are interior angles
- ∠B ∠E ∠H ∠C are interior angles
- ∠B and ∠E, ∠H and ∠C are consecutive interior angles
- ∠A and ∠G, ∠F and ∠D are alternate exterior angles
- ∠E and ∠C, ∠H and ∠B are alternate interior angles
- ∠A and ∠E, ∠C and ∠G are corresponding angles
- ∠D and ∠H, ∠F and ∠B are corresponding angles
Two lines are perpendicular if they intersect in a right angle. The axes of a coordinate plane is an example of two perpendicular lines.
In our next class, we will be talking about Calculation of Range, Median and Mode of Ungrouped Data. We hope you enjoyed the class.
Should you have any further question, feel free to ask in the comment section below and trust us to respond as soon as possible.
Ready to make school management and growth easy? Book your free onboarding session nowGet more class notes, videos, homework help, exam practice on Android [DOWNLOAD]
Get more class notes, videos, homework help, exam practice on iPhone [DOWNLOAD]