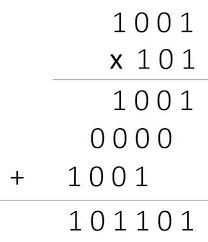Back to: Mathematics Primary 6
HELLO, WELCOME BACK TO CLASS
Our everyday numbers like 1, 2, 3, 4, 5, 6 etc. are in base 10. This means we use a decimal number system. However, these numbers can be converted from base 10 to a number in other bases. Today we will look at converting numbers is base 10 to base 2 and vice versa,
Base 2 is also called Binary and it is composed of only 0’s and 1’s.
There are several traditional methods of converting the numbers from binary to decimal but we will be looking at the expanded method.
Example: Convert 1011001012 to the corresponding base-ten number
I will list the digits in order, as they appear in the number, they’ve given me. Then, in another row, I’ll count these digits off from the RIGHT, starting with zero:
| digits: | 1 | 0 | 1 | 1 | 0 | 0 | 1 | 0 | 1 |
| numbering: | 8 | 7 | 6 | 5 | 4 | 3 | 2 | 1 | 0 |
The first row above (labelled “digits”) contains the digits from the binary number; the second row (labelled “numbering”) contains the power of 2 (the base) corresponding to each digit. I will use this listing to convert each digit to the power of two that it represents:
1×28 + 0×27 + 1×26 + 1×25 + 0×24 + 0×23 + 1×22 + 0×21 + 1×20
= 1×256 + 0×128 + 1×64 + 1×32 + 0×16 + 0×8 + 1×4 + 0×2 + 1×1
= 256 + 64 + 32 + 4 + 1
= 357
Then 1011001012 converts to 35710.
Converting decimal numbers to binaries is nearly as simple: just divide by 2
Example: Convert 35710 to the corresponding binary number.
To do this conversion, I need to divide repeatedly by 2, keeping track of the remainders as I go. Watch below:
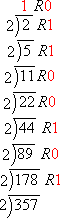
35710 converts to 1011001012.
In the above example, i divided upwards, but you can also divide downwards like this
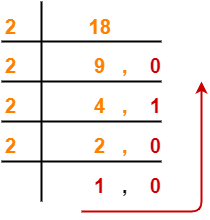
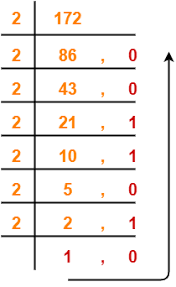
so, 1810 is 100102 17210 = 101011002
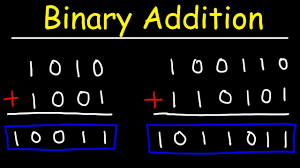
Addition of binary numbers
Binary addition is much like your normal everyday addition (decimal addition), except that it carries on a value of 2 instead of a value of 10. For example: in decimal addition, if you add 8 + 2 you get ten, which you write as 10; in the sum this gives a digit 0 and a carry of 1. Something similar happens in binary addition when you add 1 and 1; the result is two (as always), but since two is written as 10 in binary, we get, after summing 1 + 1 in binary, a digit 0 and a carry of 1.
Therefore, in binary:
0 + 0 = 0
0 + 1 = 1
1 + 0 = 1
1 + 1 = 10 (which is 0 carry 1)
Example:
ACTIVITY
Convert the following
- 8510 to base 2
- 4210 to base 2
- 101102 to base 10
- 1110012 to base 10
Add:
- 110 + 111
- 1001 + 0101
- 11110 + 01001
Subtraction of Binary Numbers
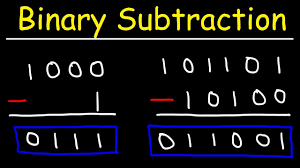
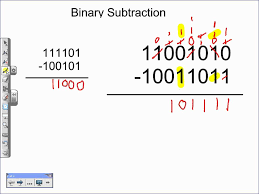
Please note that because we are subtracting in base 2, every 1 that is borrowed is counted as 2
Multiplication of Binary Numbers