Back to: MATHEMATICS SS1
Welcome to class!
In today’s class, we will be talking about the triangle: drawing and bisection of a line segment; construction and bisection of angles. Enjoy the class!
Triangle: Drawing and Bisection of Line Segment; Construction and Bisection of Angles
Drawing and bisection of the line segment
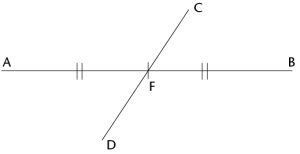
Bisecting a line segment with a ruler:
Read through the following steps.
Step 1:
Draw line segment AB and determine its midpoint.

Step 2:
Draw any line segment through the midpoint.
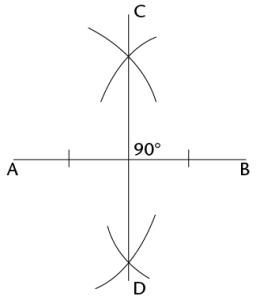
Bisecting a line segment with a compass and ruler:
Read through the following steps.
Step 1:
Place the compass on one endpoint of the line segment (point A). Draw an arc above and below the line. (Notice that all the points on the arc above and below the line are the same distance from point A.)

Step 2:
Without changing the compass width, place the compass on point B. Draw an arc above and below the line so that the arcs cross the first two. (The two points where the arcs cross are the same distance away from point A and point B.)

Step 3:
Use a ruler to join the points where the arcs intersect. This line segment (CD) is the bisector of AB.
Construction and bisection of angles
Bisecting angles without a protractor:
Read through the following steps.
Step 1:
Place the compass on the vertex of the angle (point B). Draw an arc across each arm of the angle.

Step 2:
Place the compass on the point where one arc crosses an arm and draw an arc inside the angle. Without changing the compass width, repeat for the other arm so that the two arcs cross.
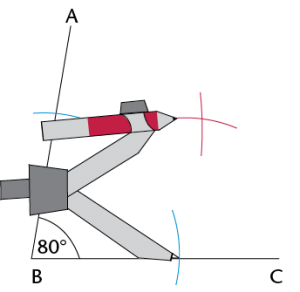
Step 3:
Use a ruler to join the vertex to the point where the arcs intersect (D).
DB is the bisector of \(\hat{ABC}\).
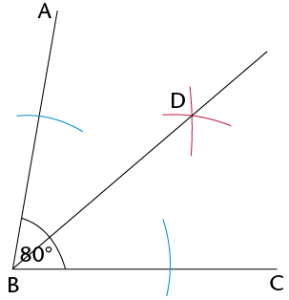
Use your compass and ruler to bisect the angles below.
Constructing special angles without a protractor
Read through the following steps.
Step 1:
Draw a line segment (JK). With the compass on point J, draw an arc across JK and up over above point J.

Step 2:
Without changing the compass width, move the compass to the point where the arc crosses JK, and draw an arc that crosses the first one.
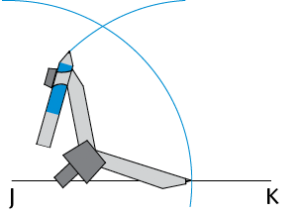
Step 3:
Join point J to the point where the two arcs meet (point P). \(\hat{PJK}\) = 60°

In our next class, we will be talking about Construction: Construction of Quadrilateral Polygon; Construction of Equilateral Triangle; Locus of Moving Points. We hope you enjoyed the class.
Should you have any further question, feel free to ask in the comment section below and trust us to respond as soon as possible.

thanks