Back to: MATHEMATICS SS1
Welcome to class!
In today’s class, we will be talking about Volumes of a frustum of cone, rectangular-based pyramid and other pyramids. Enjoy the class!
Volumes of Frustum of Cone, Rectangular-Based Pyramid and Other Pyramid
Volumes of Frustum Of Cone
A frustum may be formed from a right circular cone by cutting off the tip of the cone with a cut perpendicular to the height, forming a lower base and an upper base that are circular and parallel. The problem can be generalized to other cones and n-sided pyramids but for the moment consider the right circular cone.
Let h be the height, R the radius of the lower base, and r the radius of the upper base. One picture of the frustum is the following.
Given R, r, and h, find the volume of the frustum.
Conical Frustum Shape (of a right circular cone)
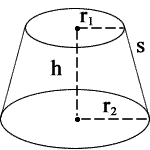
r1 = radius1
(R)r2 = radius2
h = height
s = slant height
V = volume
L = lateral surface area
T = top surface area
B = base surface area
A = total surface area
π = pi = 3.1415926535898
√ = square root
In the combination of solids, we added the volumes of two adjoining shapes which gave us the total volume of any structure. But for frustum of the cone as we are slicing the smaller end of the cone as shown in the figure, hence we need to subtract the volume of the sliced part.

The volume of the frustum of a cone
The frustum as said earlier is the sliced part of a cone, therefore for calculating the volume, we find the difference of volumes of two right circular cones.
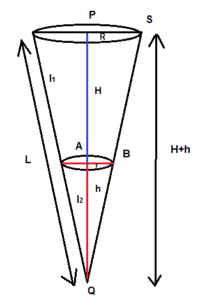
From the figure, we have, the total height H’ = H+h and the total slant height L =l1 +l2. The radius of the cone = R and the radius of the sliced cone = r.
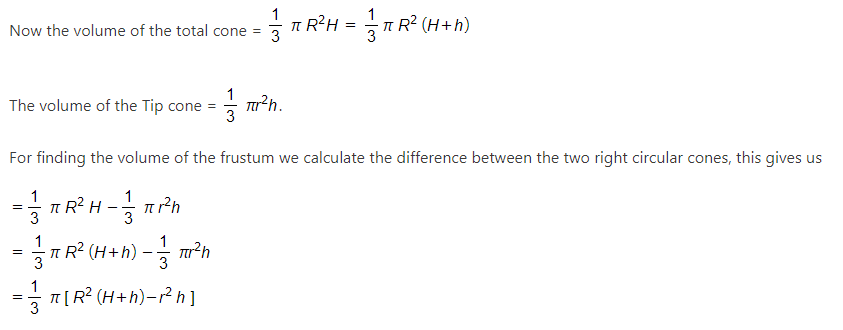
Now on seeing the whole cone with the sliced cone, we come to know that the right angle of the whole cone Δ QPS is similar to the sliced cone Δ QAB.

Rectangular-Based Pyramid
A rectangular pyramid is a three-dimensional object with a rectangle for a base and a triangular face corresponding to each side of the base. The triangular faces which are not the rectangular base are called lateral faces and meet at a point called the vertex or apex. Usually, right pyramids are studied.

Volume and Surface Area of a Rectangular Pyramid
In general, the volume of a pyramid is one-third the area of the base times the height of the pyramid.
Right Rectangular Pyramids
l: The length of the base of the pyramid
w: The width of the base of the pyramid
h: The height of the pyramid
V: The volume of the interior of the pyramid
S: The surface area of the pyramid
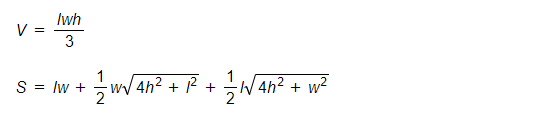
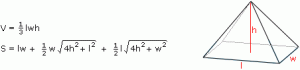
In our next class, we will be talking about Geometrical Construction. We hope you enjoyed the class.
Should you have any further question, feel free to ask in the comment section below and trust us to respond as soon as possible.

Thanks to the teacher
I really enjoyed the class
God bless you 🙏
thank you so much for this lesson it has been an enjoyable lesson to me but i dont
known others but it has been wonderful thanks so much.
Mathematics
Thanks so much for the teacher I really appreciate you ma/sir
please explain it
Thanks a lot am so grateful I love this lesson teacher god bless u ma every thing u taught me was correct I love it am happy
You tried, I really appreciate but you should have given some examples
Please i still need more help about this topic
Can you be a bit specific about what you need help with?
thanks to the teacher
please I need some examples in this frustum. but I really enjoyed the lesson thanks s lot to the tutor .
I dont understand anything
Hi Aliyah, Please what exactly is it that you don’t understand?