Back to: MATHEMATICS JSS1
Welcome to class!
In today’s class, we will be talking more about fractions. Enjoy the class!
Fractions
Multiplication and division of fractions
Multiplying fractions:
Three simple steps are required to multiply two fractions:
- Step 1: Multiply the numerators from each fraction by each other (the numbers on top). The result is the numerator of the answer.
- Step 2: Multiply the denominators of each fraction by each other (the numbers on the bottom). The result is the denominator of the answer.
- Step 3: Simplify or reduce the answer.
Examples of multiplying fractions:
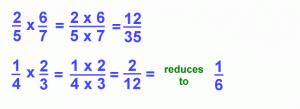
In the first example, you can see that we multiply the numerators 2 x 6 to get the numerator for the answer, 12. We also multiply the denominators 5 x 7 to get the denominator for the answer, 35. In the second example, we use the same method. In this problem, the answer we get is 2/12 which can be further reduced to 1/6.
Multiplying different types of fractions:
The examples above multiplied proper fractions. The same process is used to multiply improper fractions and mixed numbers. There are a couple of things to watch out for with these other types of fractions.
Improper fractions – With improper fractions (where the numerator is greater than the denominator) you may need to change the answer into a mixed number. For example, if the answer you get is 17/4, your teacher may want you to change this to the mixed number 4 ¼.
Mixed numbers – Mixed numbers are numbers that have a whole number and a fraction, like 2 ½. When multiplying mixed numbers, you need to change the mixed number into an improper fraction before you multiply. For example, if the number is 2 1/3, you will need to change this to 7/3 before you multiply.
You may also need to change the answer back to a mixed number when you are done multiplying.
Example:
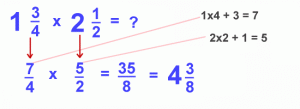
In this example, we had to change 1 ¾ to the fraction 7/4 and 2 ½ to the fraction 5/2. We also had to convert the multiplied answer to a mixed number at the end.
Dividing fractions:
Dividing fractions is very similar to multiplying fractions; you even use multiplication. The one change is that you have to take the reciprocal of the divisor. Then you proceed with the problem just as if you were multiplying.
- Step 1: Take the reciprocal of the divisor.
- Step 2: Multiply the numerators.
- Step 3: Multiply the denominators.
- Step 4: Simplify the answer.
Taking the reciprocal: To get the reciprocal, invert the fraction. This is the same as taking 1 divided by the fraction. For example, if the fraction is 2/3 then the reciprocal is 3/2.
Examples:
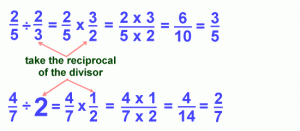
In our next class, we will be talking more about Estimation. We hope you enjoyed the class.
Should you have any further question, feel free to ask in the comment section below and trust us to respond as soon as possible.
Get more class notes, videos, homework help, exam practice on Android [DOWNLOAD]Get more class notes, videos, homework help, exam practice on iPhone [DOWNLOAD]