NUMBER BASES

Back to: MATHEMATICS JSS1

 

Welcome to class! 

In today’s class, we will be talking about number bases. Enjoy the class!

NUMBER BASES

• Counting in base two
• Conversion of base ten numbers to binary
• Addition and subtraction of two- or three-digits binary numbers

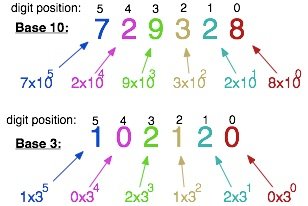
A number base is the number of digits or a combination of digits that a system of counting uses to represent numbers. A base can be any whole number greater than 0. The most commonly used number system is the decimal system, commonly known as base 10. Its popularity as a system of counting is most likely because we have 10 fingers.

Converting between binary and decimal numbers is fairly simple, as long as you remember that each digit in the binary number represents a power of two.

• Convert 101100101₂ to the corresponding base-ten number:

I will list the digits in order, as they appear in the number, they’ve given me. Then, in another row, I’ll count these digits off from the RIGHT, starting with zero:

digits:	1	0	1	1	0	0	1	0	1
numbering:	8	7	6	5	4	3	2	1	0

The first row above (labelled “digits”) contains the digits from the binary number; the second row (labelled “numbering”) contains the power of 2 (the base) corresponding to each digit. I will use this listing to convert each digit to the power of two that it represents:

• 1×2⁸ + 0×2⁷ + 1×2⁶ + 1×2⁵ + 0×2⁴ + 0×2³ + 1×2² + 0×2¹ + 1×2⁰ = 1×256 + 0×128 + 1×64 + 1×32 + 0×16 + 0×8 + 1×4 + 0×2 + 1×1

= 256 + 64 + 32 + 4 + 1

= 357

Then 101100101₂ converts to 357₁₀.

Converting decimal numbers to binaries is nearly as simple: just divide by 2.

• Convert 357₁₀ to the corresponding binary number:

To do this conversion, I need to divide repeatedly by 2, keeping track of the remainders as I go. Watch below:

As you can see, after dividing repeatedly by 2, I ended up with these reminders:

These remainders tell me what the binary number is. I read the numbers from around the outside of the division, starting on top with the final value and its remainder, and wrapping my way around and down the right-hand side of the sequential division.

Then: 357₁₀ converts to 101100101₂.

Binary Addition and Subtraction

The addition and subtraction of the binary number system are similar to that of the decimal number system. The only difference is that the decimal number system consists of the digit from 0-9 and their base is 10 whereas the binary number system consists only two digits (0 and 1) which make their operation easier. The addition and subtraction of binary number systems are explained below in details.

For understanding, the binary addition first considers the addition of two decimal numbers as shown below.

When we added the one’s column of the binary digit (i.e., 7+4) we get the number which is greater than the base of the decimal number (the base of the number is 10 and the sum of the digit is 11). Now add the tens column of the binary digit whose sum is equal to 9, and hence less than the base. So, there is no carry in the ten’s column of the binary digit.

The solution of the above sum is explained below.

• Binary addition:

The binary number system uses only two digits 0 and 1 due to which their addition is simple. There are four basic operations for binary addition, as mentioned above.

0+0=0
0+1=1
1+0=1
1+1=10

The above first three equations are very identical to the binary digit number. The column by column addition of binary is applied below in details. Let us consider the addition of 11101 and 11011.

The above sum is carried out by the following step

1 + 1 = 10 = 0 with a carry of 1.

1+0+1 = 10 = 0 with a carry of 1

1+1+0 = 10 = 10 = 0 with a carry of 1

1+1+1= 10+1 = 11= 1 with a carry of 1

1 +1 +1 = 11

Note carefully that 10 + 1 = 11, which is equivalent to two + one = three (the next binary number after 10)

Thus, the required result is 111000.

 

In our next class, we will be talking more about Number Bases.  We hope you enjoyed the class.

Should you have any further question, feel free to ask in the comment section below and trust us to respond as soon as possible.

For more class notes, homework help, exam practice, download our App HERE

Join ClassNotes.ng Telegram Community for exclusive content and support HERE