THREE DIMENSIONAL SHAPES

Back to: MATHEMATICS JSS1

 

Welcome to class! 

In today’s class, we will be talking about Wood. Enjoy the class!

THREE DIMENSIONAL SHAPES

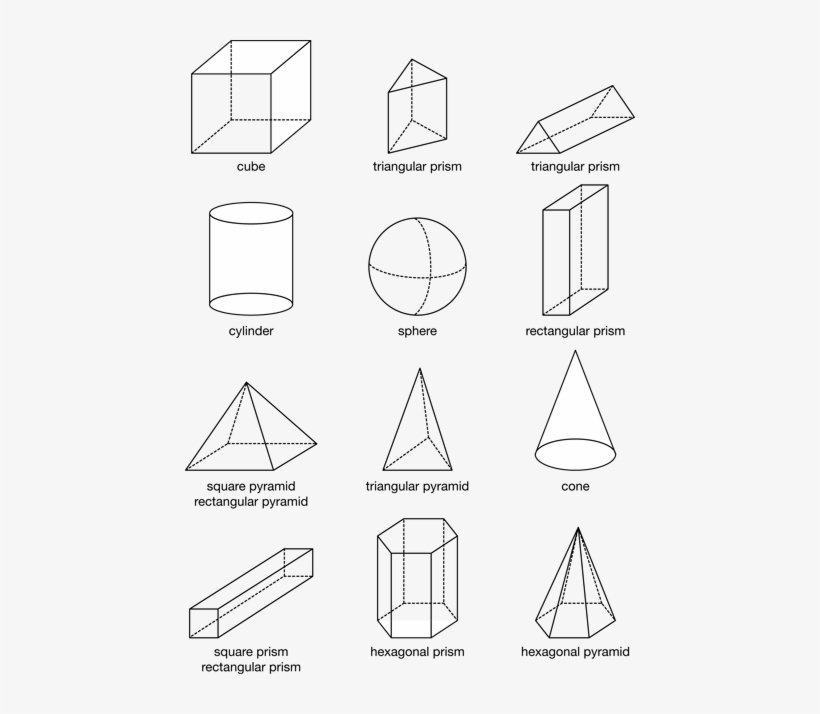
Identification of three-dimensional or 3D shapes Basic properties of cubes and cuboids, and cones Basic properties of cylinders and spheres Volume of cubes and cuboids

Surface Area and Volume of 3D shapes

The two distinct measures used for defining the 3D shapes are:

• Surface Area
• Volume

Surface Area is defined as the total area of the surface of the three-dimensional object.  It is denoted as “SA”. The surface area is measured in terms of square units. The three different classifications of surface area are defined below. They are:

• Curved Surface Area (CSA) is the area of all the curved regions
• Lateral Surface Area (LSA) is the area of all the curved regions and all the flat surfaces excluding base areas
• Total Surface Area (TSA) is the area of all the surfaces including the base of a 3D object

Volume is defined as the total space occupied by the three-dimensional shape or solid object. The volume is denoted as “V”. It is measured in terms of cubic units.

Faces, Edges, and Vertices of 3D Shapes

Three-dimensional shapes have many attributes such as vertices, faces and edges. The flat surfaces of the 3D shapes are called the faces. The line segment where two faces meet is called an edge. A vertex is a point where 3 edges meet.

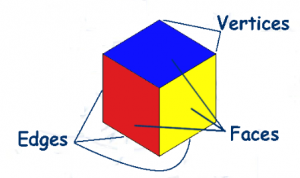
Faces, Edges, and Vertices

How to Make 3d Shapes for Maths Project

If you know what are three-dimensional shapes, it would ….be easy for you to build a 3d shape project for a house or a building. This would be easy for the students to make as they can measure the rooms easily. Rest all they need is cardboard, glue, scissors and art supplies to make it look exactly like a mini house or building. Here, we are going to discuss the list of different three-dimensional shapes with its properties and the formulas of different 3D shapes

• Cube:

A cube is a solid or three-dimensional shape which has 6 square faces. The cube has the following properties.

• All edges are equal
• 8 vertices
• 12 edges
• 6 faces

The surface area and the volume of the cube are given below:

The Surface Area of a Cube = 6a² square units

The volume of a Cube = a³  cubic units

• Cuboid:

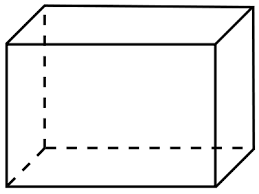
A cuboid also called a rectangular prism, where the faces of the cuboid are a rectangle in shape. All the angle measures are 90 degree

• 8 vertices
• 12 edges
• 6 faces

The surface area and the volume of the cuboid are given below:

The Surface Area of a Cuboid = 2(lb+bh+lh) Square units

The volume of a Cuboid = lbh Cubic units

• Prism:

A prism has a 3D shape which consists of two equal ends, flat surfaces or faces, and also have identical cross-section across its length. Since the cross-section looks like a triangle, the prism is generally called a triangular prism. The prism does not have any curve. Also, a prism has

• 6 vertices
• 9 edges
• 5 faces – 2 triangles and 3 rectangles

The surface area and the volume of the prism are given below:

The Surface Area of a Prism =2(Base Area) + (Base perimeter × length) square units

The volume of a Prism = Base Area × Height Cubic units

• Pyramid:

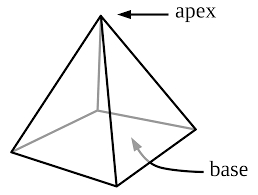
A pyramid a solid shape which has a structure, whose outer faces are triangular and meet to a single point on the top. The pyramid base can be of any shape such as triangular, square, quadrilateral or in the shape of any polygon. The most commonly used type of a pyramid is the square pyramid i.e., it has a square base and four triangular faces. Consider a square pyramid, it has

• 5 vertices
• 8 edges
• 5 faces

The surface area and the volume of the pyramid are given below:

The Surface Area of a Pyramid = (Base area) + (1/2) × (Perimeter) × (Slant height) Square units

The volume of a Pyramid = 1/ 3 × (Base Area) × height Cubic units

• Cylinder:

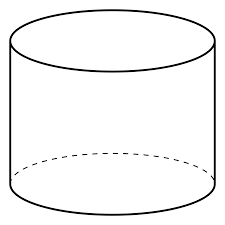
A cylinder is defined as the three-dimensional geometrical figure which has two circular bases connected by a curved surface. A cylinder has

• No vertex
• 2 edges
• 2 flat faces – circles
• 1 curved face

The surface area and the volume of the cylinder are given below:

Surface Area of a Cylinder = 2πr(h +r) Square units
The curved surface area of a cylinder = 2πrh

The volume of a Cylinder =  πr² h Cubic units

• Cone:

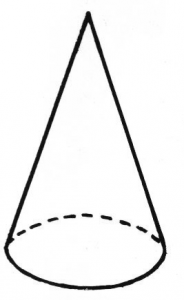
A cone is a three-dimensional object or solid, which as a circular base and has a single vertex. The cone is a geometrical figure that decreases smoothly from the circular flat base to the top point called the apex. A cone has

• 1 vertex
• 1 edge
• a flat face – circle
• 1 curved face

The surface area and the volume of the cone are given below:

The Surface Area of a Cone = πr(r +√(r²+h²) Square units
The curved surface area of a cone =πrl
Slant height of a cone = l = √(r2+h2)

The volume of a Cone = ⅓ πr²h Cubic units

• Sphere:

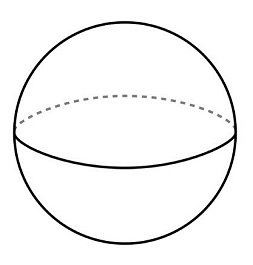
A sphere is a three-dimensional solid figure which is perfectly round in shapes and every point on its surface is equidistant from the point is called the centre. The fixed distance from the centre of the sphere is called a radius of the sphere. A sphere has

• No vertex
• 1 curved face
• No edges

The surface area and the volume of the sphere are given below:

The Curved Surface Area of a Sphere = 2πr² Square units

The Total Surface Area of a Sphere = 4πr² Square units

The volume of a Sphere = 4/3(πr³) cubic units

 

In our next class, we will be talking about Construction.  We hope you enjoyed the class.

Should you have any further question, feel free to ask in the comment section below and trust us to respond as soon as possible.

Get more class notes, videos, homework help, exam practice on Android [DOWNLOAD]

Get more class notes, videos, homework help, exam practice on iPhone [DOWNLOAD]