Application of Linear Inequalities

Back to: MATHEMATICS SS2

Welcome to class!

In today’s class, we will be talking about the application of linear inequalities. Enjoy the class!

Application of Linear Inequalities

APPLICATION OF LINEAR INEQUALITIES IN REAL LIFE

Greatest and Least Values

Example

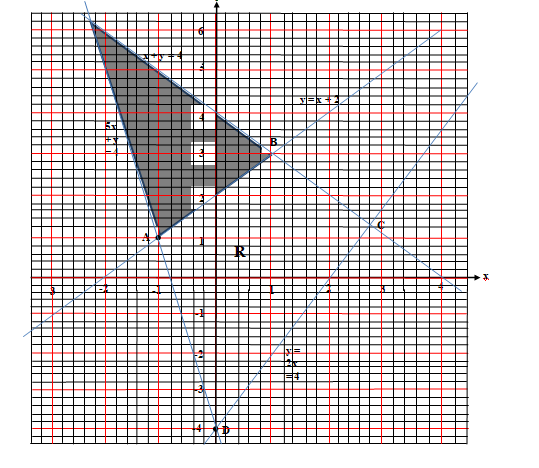
Draw a diagram to show the region which satisfies the following inequalities.

5x + y – 4, x + y 4, y x + 2, y – 2x – 4

Find the greatest and the least value of the linear function F = x + 2y within the region.

Solution

For the inequality 5x + y – 4, first draw the line 5x + y = – 4.

When x = 0, y = 4, when x = -1, y = 1

Add a third point on your own and then draw line 5x + y = -4. You may need to extend the axes to do this:

Now use a test point such as x = 0, y = 0

When x = 0, y = 0, then 0 – 4 is true, so shade the region below the line 5x + y = -4.

For the inequality x + y 4, first draw the line x + y = 4.

When x = 0, y = 4 and when y = 0, x = 4.

So draw a line that passes through (0, 4) and (4, 0).

Test point: (0, 0), so 0 4 is true. Shade the region above the line.

Similarly, for y x + 2 and y – 2x – 4, shade the unwanted regions.

The required region is labelled as R as shown. R is also called the feasible region (i.e. the region that satisfies a set of inequalities).

The greatest (maximum) and the least (minimum) of any linear function such as F = x + 2y occurs at the vertices (corner points) of the region which satisfies the given set of the inequalities.

At A(-1, 1) F = x + 2y

F = -1 + 2 = 1

At B(1, 3) F = x + 2y

F = 1 + 6 = 7

At C(2.67, 1.33) F = x + 2y

F = 2.67 + 2.66 = 5.33

At D(0, -4) F = x + 2y

F = 0 – 8 = -8

F = x + 2y is least at the point D(0, 4).

F = x + 2y is greatest at the point B(1, 3).

Note: The coordinates at point C can also be found by solving the simultaneous equations x + y = 4 and y – 2x = -4,

Example 2

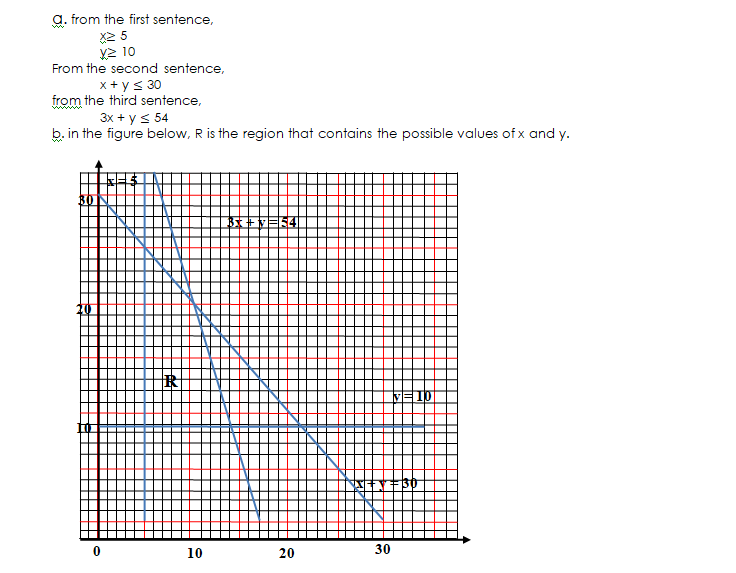
To start a new transport company, a businessman needs at least 5 buses and 10 minibuses. He is not able to run more than 30 vehicles altogether. A bus takes up 3 units of parking space, a minibus takes up to 1 unit of parking space and there are only 54 units available.

If x and y are the numbers of buses and minibuses respectively,

Write down four inequalities which represent the restrictions on the businessman
Draw a graph that shows a region representing possible values x and y.