Back to: MATHEMATICS SS2
Welcome to class!
In today’s class, we will be talking about trigonometry. Enjoy the class!
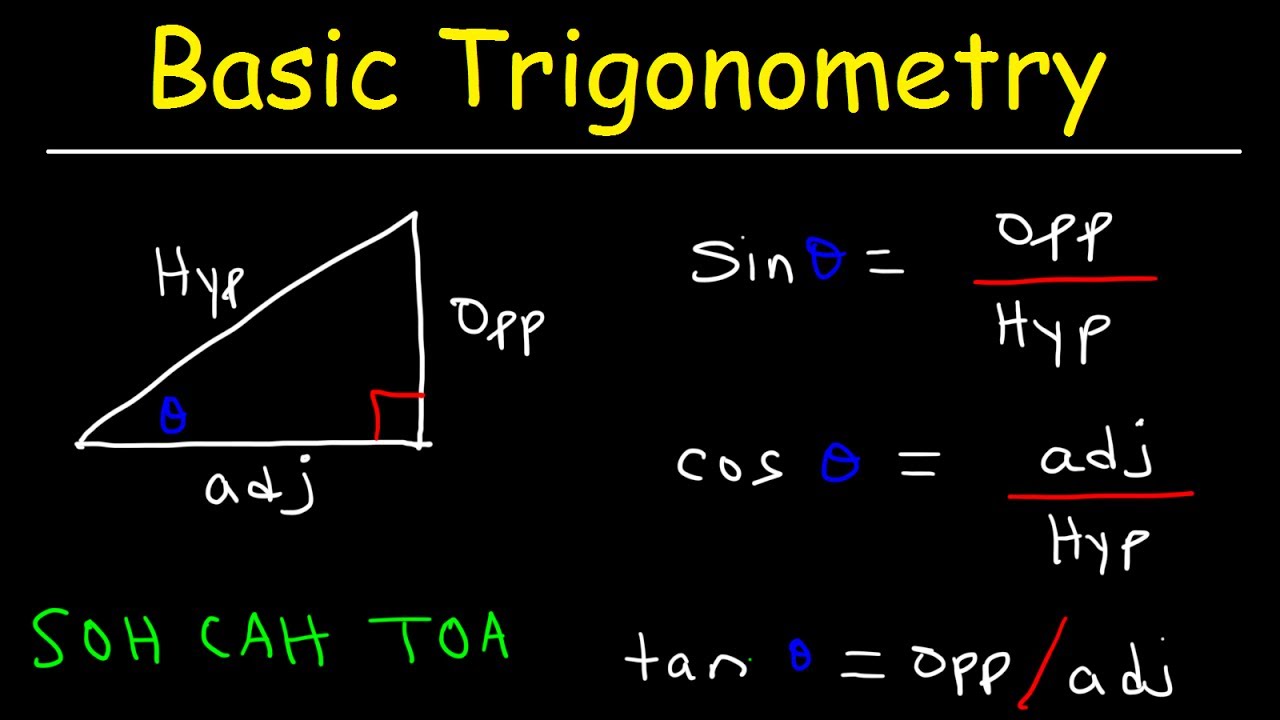
Trigonometry
Sine Rule for Acute and Obtuse Angled Triangle
Consideration is given to other triangles than a right-angled triangle. The angles of any triangle are denoted by capital letters such as; A, B, C, while the sides are represented by small letters; a, b, c, respectively.
Acute Triangle: This is a type of triangle in which the angles are less than 900.
Obtuse Triangle: Is a type of triangle in which one of the angles is more than 900 but less than 1800.
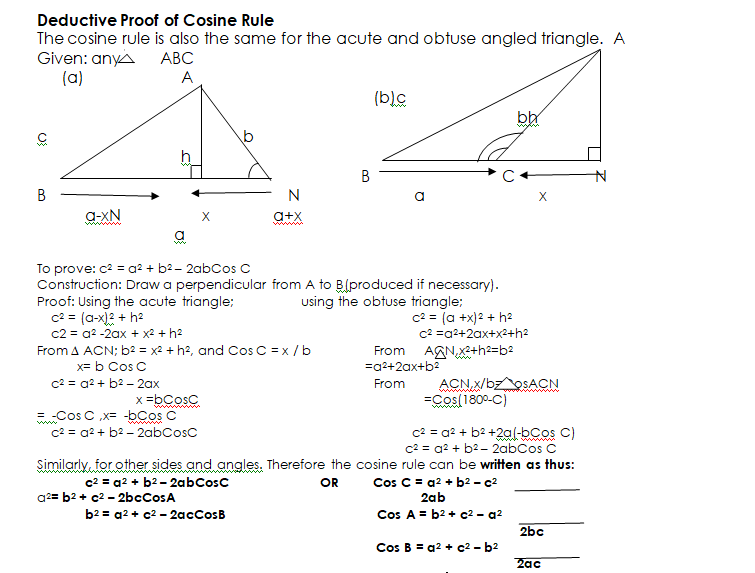
Deductive Proof of Sine Rule
The sine rule is the same for an acute and obtuse angled triangle.
Given: Any triangle ABC (acute-angled or obtuse-angled triangle).
General Evaluation
- Calculate the smallest angle in the triangle PQR such that p = 7.92m, q= 15.9m and c= 8.44m.
- Calculate the length of the side opposite the given angle in ∆ XYZ given that x =13.1m, y = 24.2m and Z = 47.80.
In our next class, we will be talking about Bearing and Distances. We hope you enjoyed the class.
Should you have any further question, feel free to ask in the comment section below and trust us to respond as soon as possible.
Get more class notes, videos, homework help, exam practice on Android [DOWNLOAD]Get more class notes, videos, homework help, exam practice on iPhone [DOWNLOAD]
Cool👏