Logarithm of Numbers Greater than and Less than One

Back to: MATHEMATICS SS2

 

Welcome to class! 

In today’s class, we will be talking about the logarithm of numbers greater than and less than One. Enjoy the class!

The Logarithm of Numbers Greater than and Less than One

CONTENT

• Standard forms
• The logarithm of numbers greater than one
• Multiplication and divisions of numbers greater than one using Logarithm
• Using logarithm to solve problems with roots and powers (no > 1)
• The logarithm of numbers less than one.
• Multiplication and division of numbers less than one using Logarithm
• Roots and powers of numbers less than one using Logarithm

STANDARD FORMS

A way of expressing numbers in the form A x 10^x where 1< A < 10 and x is an integer, is said to be a standard form. Numbers are grouped into two. Large and small numbers. Numbers greater than or equal to 1 are called large numbers. In this case, the x, which is the power of 10 is positive. On the other hand, numbers less than 1 are called small numbers. Here, the integer is negative.

Numbers such as 1000 can be converted to its power of ten in the form 10^x where x can be termed as the number of times the decimal point is shifted to the front of the first significant figure i.e. 10000 = 10

Note: One-tenth; one hundredth, etc. are expressed as negative powers of 10 because the decimal point is shifted to the right while that of whole numbers are shifted to the left to be after the first significant figure.

Examples

1. Express in standard form (i) 0.08356 (ii) 832.8 in standard form

Solution

i            0. 08356 = 8.356 x 10^-2

ii             832.8     =   8.328 x 10²

2. Express the following in standard form

(a)      39.32  =          3.932  x 10¹

(b)      4.83    =          4.83    x 10⁰

(c)       0.005321 =    5.321 x 10^-3

WORKING IN STANDARD FORM

Example:

Evaluate the following leaving your answer in standard form

1. 4.72 x 10³ + 3.648 x 10³
2. 6.142 x  10⁵ + 7.32 x 10⁴
3. 7.113 x 10^-5– 8.13 x 10^-6

solution

(1)   4.72 x 10³ + 3.648 x 10³

= [4.72 + 3.648 ] x 10³

= 8.368 x 10 ³  

(2)    6.142 x 10⁵+ 7.32 x 10⁴

=   6.142 x 10⁵+ 0.732 x 10⁵

=  [6.142 + 0.732 ] x 10⁵

= 6.874 x 10⁵

(3)     7.113 x 10^-5 – 8.13 x 10^-6

=    7.113 x 10^-5 – 0.813 x 10^-5

=  [ 7.113 – 0.813 ] x 10^-5

=  6.3 x 10^-5

Example: Simplify: √ [P/Q], leaving your answer in standard form given that

P = 3.6 x 10^-3 and

Q = 4 x 10^-8.

Solution

If a number is in its standard form, its power is its integer i.e. the integer of its logarithm e.g. log 7853 has integer 3 because 7853 = 7.853 x 10³

Examples:

Use tables (log) to find the complete logarithm of the following numbers.

(a)  80030              (b) 8      (c) 135.80

Solution

(a)            80030 =          4.9033

(b)            8          =          0.9031

(c) 13580 =          2.1329

Evaluation

Use the table to find the complete logarithm of the following:

(a)  183      (b) 89500     (c) 10.1300      (d) 7

Multiplication and Division of numbers greater than one using Logarithm

To multiply and divide numbers using logarithms, first express the number as logarithm and then apply the addition and subtraction laws of indices to the logarithms. Add the logarithm when multiplying and subtract when dividing

LOGARITHM OF NUMBERS LESS THAN ONE

To find the logarithm of a number less than one, use negative power of 10 e. g.

0.037  =          3.7 x 10^-2

=           10 ^{0.5682 x} 10^-2

=           10 ^{0.5682 + (-2)}

=           10^{-2 5682}

Log 0.037  = 2 . 5682 

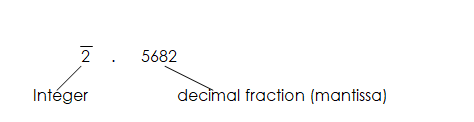
Example: Find the complete log of the following.

(a)      0.004863     (b)  0. 853    (c)  0.293

Solution

Log 0.004863                        =           3.6369

Log 0.0853                =          2.9309

Log 0.293                  =          1.4669

Evaluation

1. Find the logarithm of the following:

(a)    0.064       (b)   0.002     (c) 0.802

2. Evaluate using logarithm.

$\frac{95.3 \times 318.4}{1.{29}^5 \times 2.03}$

USING LOGARITHM TO EVALUATE PROBLEMS OF MULTIPLICATION, DIVISION, POWERS AND ROOTS WITH NUMBERS LESS THAN ONE

OPERATION WITH BAR NOTATION

Note the following when carrying out operations on the logarithm of negative numbers.

1.  The mantissa (fractional part) is positive, so it has to be added in the usual manner.
2. The characteristic (integral part) is either positive or negative and should, therefore, be added or operated as directed numbers.
3. For operations like multiplication and division, separate the integer from the characteristic before performing the operation.

 

In our next class, we will be talking about Percentage Error.  We hope you enjoyed the class.

Should you have any further question, feel free to ask in the comment section below and trust us to respond as soon as possible.

How Can We Make ClassNotesNG Better - CLICK to Tell Us💃

Pass WAEC, JAMB, NECO, BECE In One Sitting CLICK HERE!

Watch FREE Video Lessons for Best Grades & Academic Success💃