Application of Surds to Trigonometric Ratios

Back to: MATHEMATICS SS3

Welcome to class! 

In today’s class, we will be talking about the application of surds to trigonometric ratios. Enjoy the class!

Application of surds to trigonometric ratios

Apart from solving quadratics, surds also arise in trigonometry.

The angles 30°, 45°, 60° have the following trigonometric ratios.

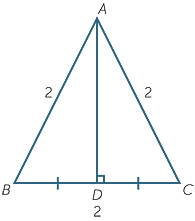
Triangle ABC is equilateral. AD is the line interval from A to the midpoint of BD. Triangles ABD and ACD are congruent (SSS).

$Angles ABD =60°, BAD = 30° and Pythagoras’ theorem gives that AD=\surd 3$

Hence,

	sin 30° = cos 60° = 1/2 ,		sin 60° = cos 30° = $\surd 3/2$ ,
	tan 30° = $1/\surd 3$  and		tan 60° = $\surd 3$ .

$U\sin g a square divided by a diagonal we form two isosceles right–angled triangles and can see \sin 45° = \cos 45° = 1/\surd 2 and \tan 45° = 1.$

The trigonometric functions of y = cos θ and y = cos θ.

$U\sin g the values \sin 30° = 1/2 = 0.5 and \sin 60° =\surd 3/2\approx 0.87, we can draw up the following table of values and then plot them.$

θ°		0		30		60		90		120		150		180		210		240		270		300		330		360
sin θ		0		0.5		0.87		1		0.87		0.5		0		−0.5		−0.87		−1		−0.87		−0.5		0

More points can be used to show that the shape of the graph is as shown below.

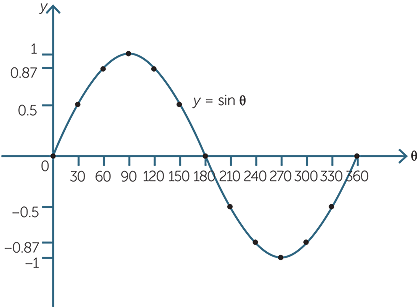
Electrical engineers and physicists call this a sine wave.

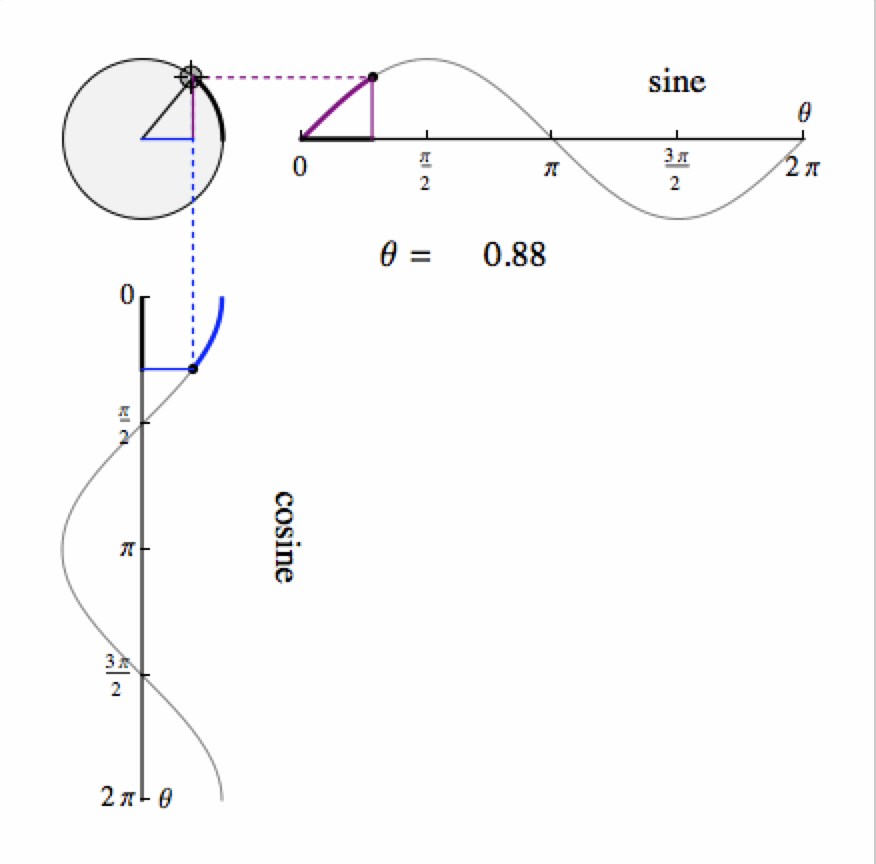
The basic formulae here all reply on the SINE graph as follows:

• The sine of an angle is defined by the vertical height of a point as it rotates around a unit circle (that is, its radius is 1) measured from a horizontal line through the centre of the circle. So it cannot be bigger than 1 or less than -1.
• the cosine of an angle is defined by the horizontal distance of a point as it rotates around the unit circle measured from a vertical line through the centre of the circle. It too must be in the range -1 to 1.

The surd form of trigonometric ratios:

The equilateral triangle above has sides each 2 units long and all angles at 60^o. It has been halved into 2 right – angled triangles of base 1 unit long. Using Pythagoras:

(ab)² = (ac)² + (bc)²
=> (2)² = (ac)² + (1)²
=> (ac)² = 4 – 1 = 3
and (ac) = root 3.

Using the definitions of trigonometric ratios, summarised in SOHCAHTOA:

sin 30^o = bc / ab = 1 / 2
sin 60^o = ac / ab = root 3 / 2
cos 30^o = ac / ab = root 3 / 2
cos 60^o = bc / ab = 1 /2
tan 30^o = bc / ac = 1 / root 3
tan 60 = ac / bc = root 3 / 1 = root 3

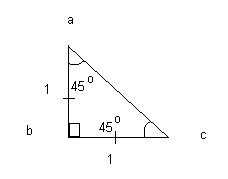
The isosceles above has equal sides of 1 unit each and the 2 complementary angles each of 45^o. Using Pythagoras’ Theorem to find side (ac):

(ac)² = (ab)² + (bc)²
(ac)² = (1)² + (1)² = 2
ac = root 2

Trigonometrical ratio:	Surd form:	Approximation
sin 30o	1 / 2	0.5
sin 45o	1 / root 2	0.7071
sin 60o	root 3 / 2	0.866
cos 30o	root 3 / 2	0.866
cos 45	1 / root 2	0.7071
cos 60o	1 / 2	0.5
tan 30o	1 / root 3	0.5774
tan 45o	1
tan 60o	root 3	1.7321

For any pair of complementary angles these 2 rules apply:

sin x = cos (90 – x)
and cos x = sin (90 – x)

sin 30o = cos 60o

sin 60o = cos 30o

sin 45o = cos 45o

sin 20o = cos 70o

cos 41o = sin 49o

cos 72o = sin 18o

sin 36o = cos 54o

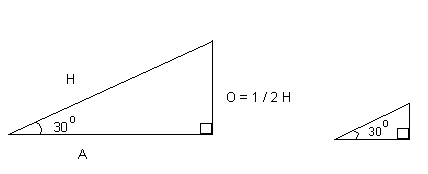
When the angle is 30^o on a right-angled triangle, then the side opposite the 30^o angle is half the hypotenuse. This is also true for similar triangles. Sides H, A and O can be any value and O = 1 / 2 H. Therefore, sin 30^o = 0.5.

 

In our next class, we will be talking about Matrices and Determinant. We hope you enjoyed the class.

Should you have any further question, feel free to ask in the comment section below and trust us to respond as soon as possible.

Get more class notes, videos, homework help, exam practice on Android [DOWNLOAD]

Get more class notes, videos, homework help, exam practice on iPhone [DOWNLOAD]