Back to: MATHEMATICS SS3
Welcome to class!
In today’s class, we will be talking about Integration and evaluation of simple algebraic functions. Enjoy the class!
Integration
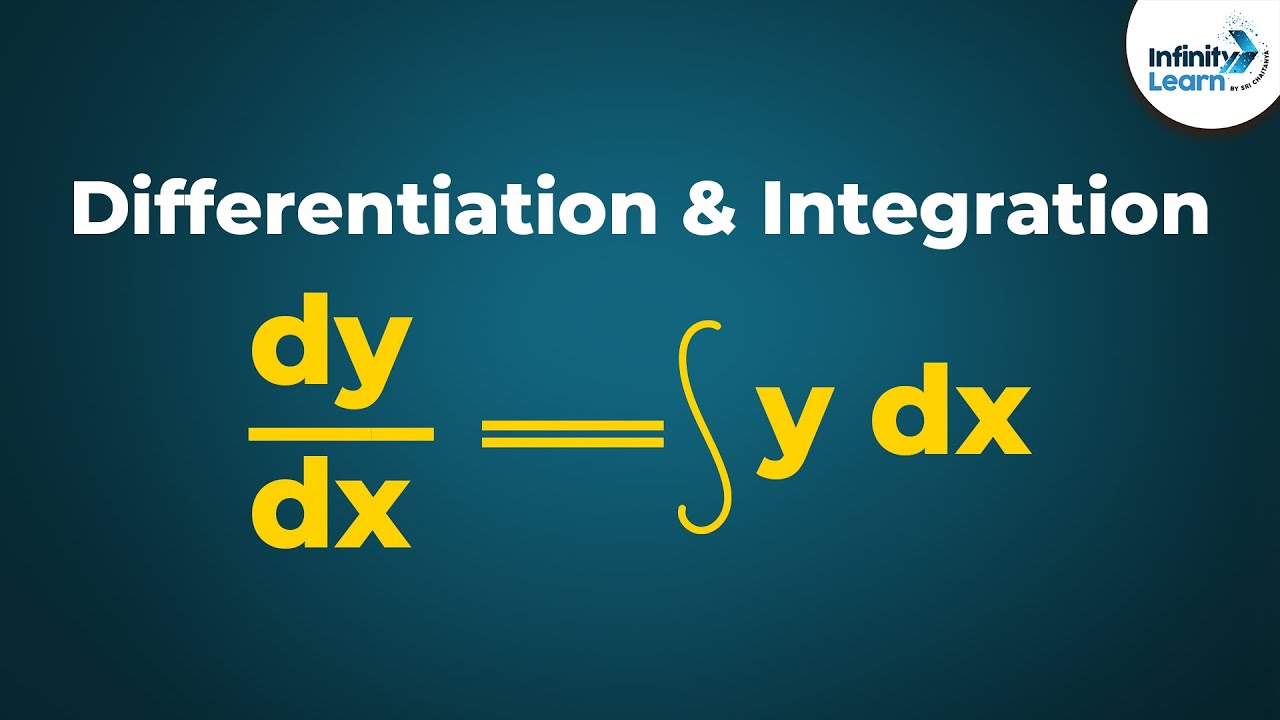
It is the reverse of differentiation. When we integrate, we have to add a constant (c).
To integrate a term, increase its power by 1 and divide by this figure. In other words:
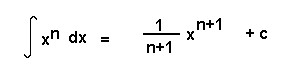
From our knowledge of derivatives, we can immediately write down a number of antiderivatives. Here is a list of those most often used:
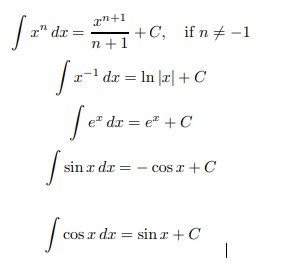
Methods of integration
1. Integration by parts:
This technique for turning one integral into another is called integration by parts.
Start with the product rule,
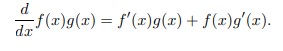
We can rewrite this as
If we let u = f(x) and v = g(x) then du = f ′ (x) dx and dv = g ′ (x) dx and
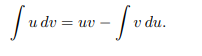
To use this technique, we need to identify likely candidates for u = f(x) and dv = g ′ (x) dx.
Example:
Let u = ln x , du = 1/x dx
let dv = x dx , v = x 2 /2
therefore,
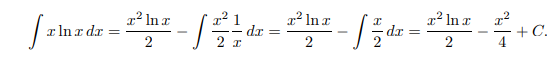
2. Partial fractions:
If the integrand (the expression after the integral sign) is in the form of an algebraic fraction and the integral cannot be evaluated by simple methods, the fraction needs to be expressed in partial fractions before integration takes place.
The steps needed to decompose an algebraic fraction into its partial fractions results from a consideration of the reverse process − addition (or subtraction).
Consider the following addition of algebraic fractions:
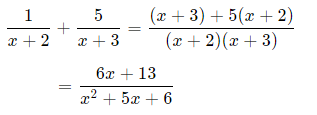
We want to go the other way around i.e. if we were to start with the expression
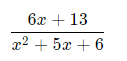
and try to find the fractions whose sum gives this result, then the two fractions obtained, i.e.
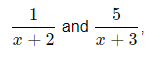
are called the partial fractions of
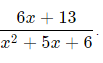
So, if we needed to integrate this fraction, we could simplify our integral in the following way:
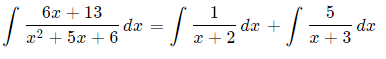
We integrate the two fractions using what we learned in Basic Logarithmic Form:
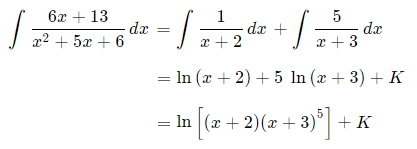
Where K is the constant.
3. Substitution:
The substitution method (also called u−substitution) is used when an integral contains some function and its derivative.
In this case, we can set u equal to the function and rewrite the integral in terms of the new variable u. This makes the integral easier to solve.
Do not forget to express the final answer in terms of the original variable x. Substitution for integrals corresponds to the chain rule for derivatives.
Suppose that F(u) is an antiderivative of f(u):
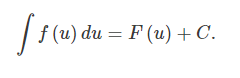
If u = u(x) is a differentiable function and using the chain rule, we have
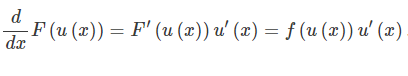Integrating both sides,
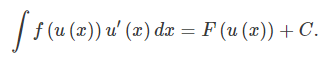Therefore,
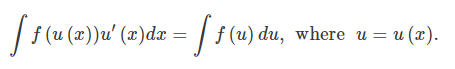
This is the substitution rule formula for indefinite integrals.
Note that the integral on the left is expressed in terms of the variable x. The integral on the right is in terms of u.
Example:
Find the integral ∫(3x+2)5dx.
Solution
We make the substitution u = 3x+2.
Then
du = d(3x+2) = 3dx.
So, the differential dx is given by
dx = du / 3
Therefore,
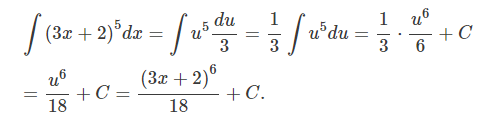
Area under a curve
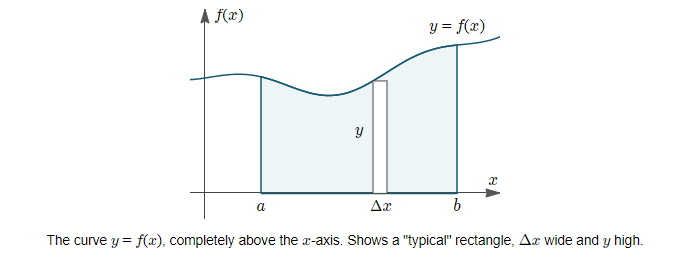
In this case, we find the area by simply finding the integral:
Example:
Find the area bounded by y = x2 − 4, the x-axis and the lines x = −1 and x = 2.
Solution
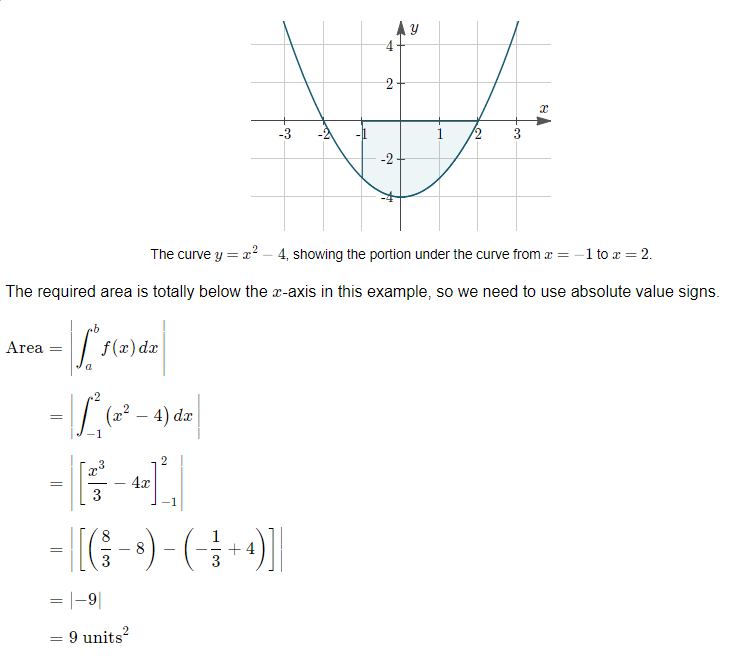
Simpson’s rule
In Simpson’s Rule, we will use parabolas to approximate each part of the curve. This proves to be very efficient since it’s generally more accurate than the other numerical methods we’ve seen.
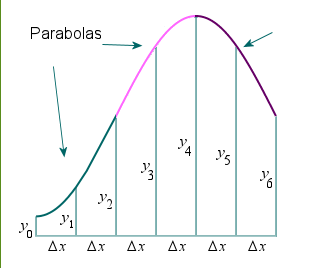
We divide the area into n equal segments of width Δx. The approximate area is given by the following:
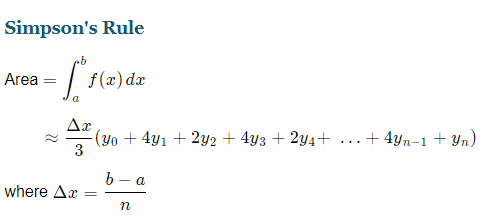
Note: In Simpson’s Rule, n must be EVEN.
We hope you enjoyed the class.
Should you have any further question, feel free to ask in the comment section below and trust us to respond as soon as possible.
Get more class notes, videos, homework help, exam practice on Android [DOWNLOAD]Get more class notes, videos, homework help, exam practice on iPhone [DOWNLOAD]