Differentiation of algebraic functions

Welcome to class!

In today’s class, we will be talking about differentiation of algebraic functions. Enjoy the class!

Differentiation of algebraic functions

What is differentiation?

Differentiation is all about finding rates of change of one quantity compared to another. We need differentiation when the rate of change is not constant.

Algebraic functions:

An algebraic function is a function that can be written using a finite number of the basic operations of arithmetic (i.e., addition, multiplication, and exponentiation).

In order to take the derivative of these functions, we will need the power rule.

The power rule:

The power rule states that if f (x) = xⁿ, then f ′(x) = nxⁿ⁻¹.

Rules of differentiation for algebraic functions

In this tutorial we will discuss the basic formulas of differentiation for algebraic functions.

$d / d x (c) = 0, w h e r e c i s a n y c o n s \tan t .$ $d / d x (x) = 1 d / d x (c x) = c, w h e r e c i s a n y c o n s \tan t . d / d x x n = n x n - 1, w h i c h i s k n o w n a s t h e p o w e r r u l e o f a d e r i v a t i v e .$

Differentiation from first principles

We know that the gradient of the tangent to a curve with equation y = f(x) at x = a can be determined using the formula:

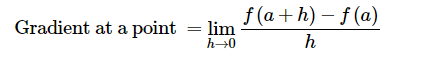
We can use this formula to determine an expression that describes the gradient of the graph (or the gradient of the tangent to the graph) at any point on the graph. This expression (or gradient function) is called the derivative.

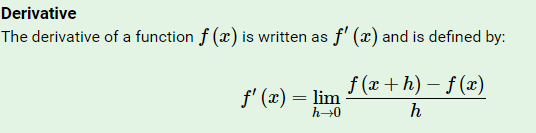
Notation

There are a few different notations used to refer to derivatives. It is very important that you learn to identify these different ways of denoting the derivative and that you are consistent in your usage of them when answering questions.

If we use the common notation y=f(x), where the dependent variable is y and the independent variable is x, then some alternative notations for the derivative are as follows:

f ′ (x) = y′ = dy/dx = df/dx = d/dx [f(x)] = Df(x) = D_xy

The symbols D and d/dx are called differential operators because they indicate the operation of differentiation dy/dx means y differentiated with respect to x. Similarly, dp/dx means p differentiated with respect to x.

Important: dy/dx is not a fraction and does not mean dy ÷ dx.

Example:

Derivative of a sum

d (u + v)/dx = du/dx + dv/dx

Here, u and v are functions of x. The derivative of the sum is simply equal to the derivative of the first plus derivative of the second. It does not work the same for the derivative of the product of two functions, that we meet in the next section.

Example:

If u = x² and v = x⁹, then:

d (u + v)/dx = du/dx + dv/dx

= d(x²)/dx + d(x⁹)/ dx

=2x+9x⁸

The Derivative of Basic Functions:

You can work out the derivative of tan(x) using the quotient rule, and the derivatives of the inverse trig functions arc-sine, arc-cosine, etc., with implicit differentiation.

In our next class, we will be talking more about Differentiation of algebraic functions. We hope you enjoyed the class.

Should you have any further question, feel free to ask in the comment section below and trust us to respond as soon as possible.

For more class notes, homework help, exam practice, download our App HERE

Join ClassNotes.ng Telegram Community for exclusive content and support HERE

Differentiation of algebraic functions