Surds

Back to: MATHEMATICS SS3

Welcome to class! 

In today’s class, we will be talking about surds. Enjoy the class!

Surds

A root of a positive real quantity is called a surd if its value cannot be exactly determined. A surd is an expression that includes a square root, cube root or other root symbols.

Surds are the irrational numbers which are roots of positive integers and the value of roots cannot be determined, they cannot be written exactly in decimal form.

Surds have infinite non-recurring decimals. Examples are √2, √5, ∛17 which are square roots or cube roots or nth root of any positive integer.

A surd is an irrational root. A root (whether a square root, cube root or higher root) of any integer will either be an integer or a surd. The root will only be an integer if the original integer was a perfect power.

For example, consider square roots: the square root of an integer n will only be an integer if n itself is a perfect square number such as 1, 4, 9, 16, etc. The square root of any other integers will always be surds. So, for example, √7 is a surd and as it is irrational, its decimal expansion would go on forever without a recurring pattern.

Note that square roots of decimals or fractions are not always surds. For example, √6.25=2.5 which is rational and therefore not a surd. √1/4 = 1/2 which is also rational and therefore not a surd.

• Rational number:

A number of the form p/q, where p (may be a positive or negative integer or zero) and q (taken as a positive integer) are integers prime to each other and q not equal to zero is called a rational number or commensurable quantity.

Rational numbers are the numbers which can be expressed in the form of p/q where p is a positive or negative integer or zero and q is a positive or negative integer but not equal to zero.

Like: 3/7, 3, -2/3 are examples of rational numbers.

For example, each of the numbers 7, 3/5, 0.73, √25 etc. is a rational number. Evidently, the number 0 (zero) is a rational number.

• Irrational number:

A number which cannot be expressed in the form p/q where p and q are integers and q ≠ 0, is called an irrational number or incommensurable quantity.

Irrational numbers are the numbers which can’t be expressed in the form of p/q where p and q are integers and q ≠ 0. Irrational numbers have infinite numbers of decimals of non-recurring nature.

Like: √2, √5 are the irrational numbers.

For example, each of the numbers √7, ∛3, etc. is an irrational number.

Basic operations with surds and conjugate of binomial surds

 1. Addition or subtraction: You can only add or subtract similar or like surds:

$\surd 8+ 3\surd 2= 2\surd 2+ 3\surd 2= 5\surd 2$

2. Multiplication and division: If the surds have the same index, you can do as follows:

$\surd 2 .\surd 3= \surd 6$

3. Powers:

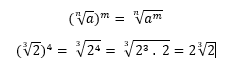
Multiplication and division of surds

When we come to multiply two surds, we simply multiply the numbers outside the square root sign together, and similarly, multiply the numbers under the square root sign, and simplify the result. A similar procedure holds for the division.

• $a\surd b \times c\surd d=ac\surd bd$
• $a\surd b \times c\surd d=ac/\surd bd$

Rationalising the denominator

$In the pre–calculator days, finding an approximation for a number such as 6/\surd 2$ $was difficult to perform by hand because it involved calculating 6/1.4142 \left(approximately\right) by long division.$

To overcome this, we multiply the numerator and denominator by  to obtain

$6/\surd 2 \times \surd 2/\surd 2= (6\surd 2)/2=3\surd 2$

Since the introduction of calculators, this is no longer necessary.

There are many occasions in which it is much more convenient to have the surds in the numerator rather than the denominator. This will be used widely in algebra and later in calculus problems.

The technique of removing surds from the denominator is traditionally called rationalising the denominator (although in practice we make the denominator a whole number).

Conjugate of binomial surds

$In the expression 1/(\surd 7+ \surd 5) , it is not obvious to remove the surds from the denominator.$

To do this, we exploit the difference of two squares identity, (a + b) (a − b) = a² − b².

$If we multiply \surd 7+\surd 5 by \surd 7–\surd 5, we obtain 7 - 5 = 2.$ $The numbers \surd 7+\surd 5 and \surd 7–\surd 5 are said to be conjugates of each other.$

Thus, the method we will employ to rationalise the denominator involving such surds is to multiply the top and bottom by the conjugate of the surd in the denominator.

 

In our next class, we will be talking about Application of surds to trigonometric ratios. We hope you enjoyed the class.

Should you have any further question, feel free to ask in the comment section below and trust us to respond as soon as possible.

Get more class notes, videos, homework help, exam practice on Android [DOWNLOAD]

Get more class notes, videos, homework help, exam practice on iPhone [DOWNLOAD]