Coordinate Geometry of a Straight Line

Back to: MATHEMATICS SS3

 

Welcome to class! 

In today’s class, we will be talking about coordinate geometry of a straight line. Enjoy the class!

Coordinate Geometry of a Straight Line

Any straight line has an equation of the form

y = mx + c

where m, the gradient, is the height through which the line rises in one-unit step in the horizontal direction

c, the intercept, is the y-coordinate of the point of intersection between the line and the y-axis. This is shown in the figure below.

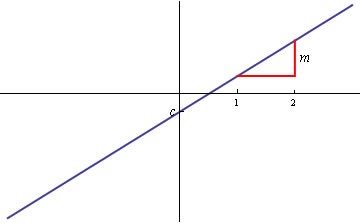
The straight line, y = mx + c

If we know the gradient m of a straight line with unknown intercept c, and the coordinates (x₁ , y₁) of a point through which it passes, then we know that

y₁ = mx₁ + c

and therefore

c = y₁ − mx₁

If we substitute into

y = mx + c

we obtain

y = mx− mx₁ + y₁

which we can rearrange to give

y− y₁ = m(x − x₁)

If we know two points (x₁ , y₁) and (x₂ , y₂) through which passes a line with unknown gradient m and intercept c, then

y₁ = mx₁ + c ,

y₂  = mx₂ + c

Subtracting the first equation from the second gives

y₂ − y₁ = m(x₂ − x₁)

and therefore

$m =(x2 – x1)/(y2 – y1)$

The equation of the line is therefore

$y - y1 = (y2 – y1)/(x2 – x1 ) (x - x1)$

The midpoint of the line joining two points

Once we know the coordinates of two points on a straight line, we can find the mid-point of the line.

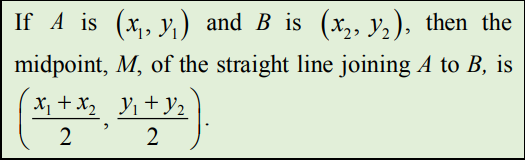
Distance between two points

The distance formula is derived from the Pythagoras theorem. To find the distance between two points, if A is (x₁ , y₁) and B is (x₂ , y₂), all that you need to do is use the coordinates of these ordered pairs.

The distance between two points is given by:

$Distance=\surd (〖(x2–x1){〗}^2+〖(y2–y1\left){〗}^2\right)$

 

In our next class, we will be talking more about the Coordinate Geometry of straight line.  We hope you enjoyed the class.

Should you have any further question, feel free to ask in the comment section below and trust us to respond as soon as possible.

For more class notes, homework help, exam practice, download our App HERE

Join ClassNotes.ng Telegram Community for exclusive content and support HERE