Coordinate Geometry of Straight Line II

Back to: MATHEMATICS SS3

Welcome to class! 

In today’s class, we will be talking about coordinate geometry of a straight line. Enjoy the class!

Coordinate Geometry of a Straight Line II

Gradient and intercepts of a line

All straight lines have a general equation of the form, where m is the gradient and c is the intercept on the vertical axis.

The gradient (m) of a line is a measure of its slope or steepness. It is defined as a ratio of its vertical displacement, to its horizontal displacement.

$m = (y2–y1)/(x2–x1)$

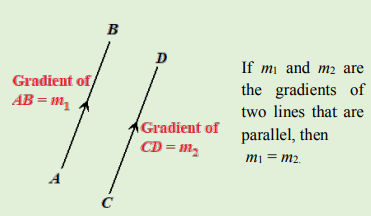
• Gradient of parallel lines:

Parallel lines have the same slope and so must have the same gradient. That is, lines that have the same gradients are parallel. We can use this fact to prove that any two straight lines are parallel or not.

m₁ = m₂

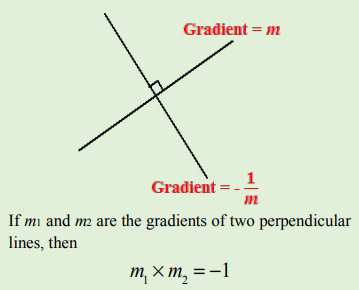
• Gradient of perpendicular lines:

The product of the gradients of perpendicular lines is equal to −1. If the product of the gradients of any two lines is −1, then the lines are perpendicular to each other. We can use this fact to prove that and two straight lines are perpendicular or not.

The angle between two intersecting straight lines

The angle between two intersecting straight lines means the measure of the acute angle between the lines.

The angle θ between the lines having slope m₁ and m₂ is given by

$\tan \theta = │(m2–m1)/(1+(m1 \times m2\left)\right)│$

 

In our next class, we will be talking about Differentiation of algebraic functions. We hope you enjoyed the class.

Should you have any further question, feel free to ask in the comment section below and trust us to respond as soon as possible.

School Owner? Looking for ready-made content and tools to save time and grow easily? Book a free demo session now

Get more class notes, videos, homework help, exam practice on Android [DOWNLOAD]

Get more class notes, videos, homework help, exam practice on iPhone [DOWNLOAD]