Properties of Waves

Welcome to class!

In today’s class, we will be talking about the properties of waves. Enjoy the class!

Waves exhibit the following properties/characteristics

Reflection:

When a wave meets a barrier in its path, it turns back if the barrier is plane; the angle of incidence is equal to the angle of reflection. This is called reflection. All waves exhibit reflection. The production of echo is due to the reflection of sound waves. The formation of an image in a mirror is due to the reflection of light waves.

Refraction:

When a wave moves from one medium to another, its direction may change at the boundary between the two media. This is called refraction. The change in direction is due to a change in wave velocity as it passes from one medium to another. A straw dipped in a glass of water appears bent due to refraction of light when it passes from air to water. Also, when one looks into a deep pool, it appears shallow because of reflection of light. It is clear from the diagram below that wavelength has changed from λ₁ to λ₂

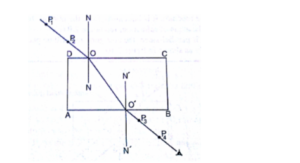
NOTE

Waves travel more slowly in shallow water (same frequency shorter wavelength). Therefore, the refractive index for water passing from deep to shallow water:

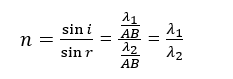
Velocity in deep water = V₁ = f λ₁

Velocity in shallow water = V₂ = f λ₂

Thus, the refraction index (n),

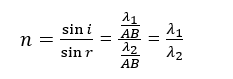
Velocity in deep water = V₁ = f λ₁

Velocity in shallow water = V₂ = f λ₂

Thus, the refraction index (n),

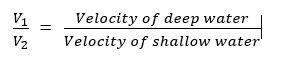
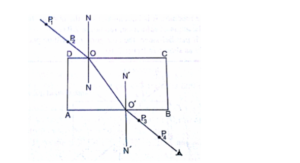
Huygens (figure 2) considered the case of plane light waves being refracted from one medium to a more optically dense medium and obtained the same result.

Interference:

When two waves moving along different path meet and intersect, interference takes place. There are two types of interference: if when the two waves interact they re-enforce each other (i.e. the combined amplitude is greater than any one of two waves) the interaction is called constructive interference, and if on the other hand, the interaction makes the waves to cancel out (neutralize) each other (i.e. the combined amplitude is zero) the interaction is called Destructive interference.

Diffraction:

The ability of a wave to bend around the edge of an obstacle or to spread around a small opening (aperture) is called diffraction. Diffraction of a wave depends on the size of the aperture relative to the wavelength of the wave. For instance, doors and windows are big apertures that can cause the diffraction of sound waves but too bid to cause diffraction of light waves. Diffraction of light requires very small aperture because the wavelength of light is very small.

Polarization:

Not all waves exhibit polarization. Only transverse waves exhibit polarization. We said earlier that in a transverse wave the vibration is perpendicular to its direction of motion. These vibrations take place along all axes in planes perpendicular to the direction of motion. If a device (means) can now cut off all vibration in all axes except one, then we say that the wave is polarized. That is vibration along one axis is perpendicular to its direction of motion and there are no other vibrations in any axis.

Plane polarization of light

A plane polarization of light means the fluctuations or a vibration that is constructed to vibrate only in one plane perpendicular to the direction of the light.

Applications of Plane Polarized light

Polarized cameras
Production of three-dimensional films
Sunglasses to reduce the intensity of light
Determination of concentration of sugar solution.

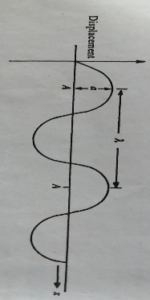
Mathematical representative of wave motion

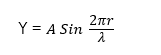
Where

Y = vertical displacement of vibrating particles

λ = wavelength between two successive crest

A = amplitude or maximum displacement

x = horizontal co-ordinate of the vibrating particle from the origin.

= phase difference of a particle at a distance x from the origin.

Plane progressive wave

An equation for a plane-progression wave may be written as:

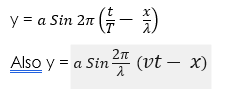
WORKED EXAMPLES

(1) Calculate the velocity of a wave whose frequency is 0.5 kHz and its wavelength is 40cm.

SOLUTION

Given parameters;

F = 0.5 kHz = 500 Hz

= 40 cm = 0.4m

V = f

V = 500 x 0.4 = 200 m/s

(2) A radio signal has a wavelength of 3m. On what frequency is it operating? (Speed of radio wave = 3 x 10⁸m/s).

SOLUTION

Given parameters;

V = 3 x 10⁸m/s

= 3m

f = =

f = 100MHz

(3) If v = 3 x 10⁸m/s, = 6 x 10^-7 m. What is the frequency?

SOLUTION

Velocity, v = frequency (f) x wavelength (λ)

V = f

f = =

f = 5 x 10¹⁴ Hz

(4) The wavelength of a water wave is 10cm and the frequency is 15Hz.

(i) What is the distance between the successive crest of the wave?

(ii) What is the speed of the wave?

(iii) What is the period of the wave?

SOLUTION

(i) The distance between successive crest of the wave is the wavelength = 10cm

(ii) Speed, v = frequency (f) x wavelength (λ)

V = f

V = 15 x 10

V = 150 cm/s or 1.5 m/s

(iii) Period, T = 0.067 s

(5) A plane progressive wave is represented by the equation

y = a sin (2000πt – )

Where the symbols have their usual meanings? Calculate

(i) The wavelength of the wave

(ii) Its speed

(iii) Its frequency

(iv) Its period and

(v) Phase difference if two layers of the wave are 180 cm apart.

SOLUTION

(i) y = a sin (2000πt – )

Where t is in seconds and, y in cm we have also that:

y =

= 2000π and =

Therefore, wavelength, λ =

Wavelength λ = 2 x 17 = 34 cm

(ii) = 2000π

Therefore, Speed, v =

Speed, v = 1000 x λ

Speed, v = 1000 x 34 = 34000 m/s

(iii) Frequency, f = = = 1000Hz

(iv) Period, T = = = 10^-3Hz

(v) Since the two layers are 180 cm apart, they are separated by

Wavelengths, or by 5Hz

Their phase difference for a separation = 2π

Hence for a separation omitting 5λ =

(6) A vibrator causes water ripples to travel across the surface of a tank. The wave travels 50 cm in 2.0s and the distance between successive crest is 5cm. calculate the frequency of the vibrator.

SOLUTION

Velocity =

= 25cm/s

The wavelength of water wave = distance between successive crest = 5 cm

But v = fλ

Therefore f =5Hz

In our next class, we will be talking about Light Wave. We hope you enjoyed the class.

Should you have any further question, feel free to ask in the comment section below and trust us to respond as soon as possible.

School Owner? Looking for ready-made content and tools to save time and grow easily? Book a free demo session now

Get more class notes, videos, homework help, exam practice on Android [DOWNLOAD]

Get more class notes, videos, homework help, exam practice on iPhone [DOWNLOAD]

Properties of Waves