Back to: PHYSICS SS2
Welcome to class!
In today’s class, we will be talking about projectiles. Enjoy the class!
Projectiles
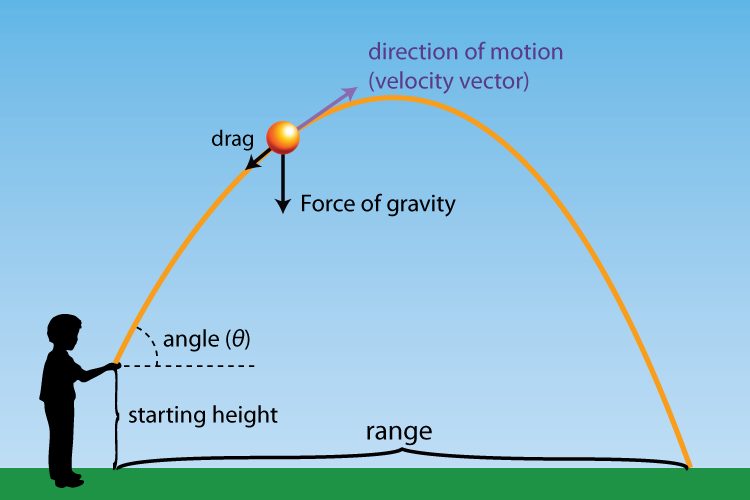
THE CONCEPTS OF PROJECTILES
Let us consider a boy who releases a piece of stone from his catapult against a bird on a tree branch, the stone will travel in a parabolic path towards the bird. Likewise, if we throw a tennis ball against a wall, the path of the ball towards the wall is a parabola. On hitting the wall, the ball returns to the ground also along a parabolic path. The same type of curve is seen when a ball is projected horizontally from the top of a building. The stone or ball been projected is known as PROJECTILE. A projectile is an object launched into the air and allowed to move on its own freely under gravity.
Examples of Projectile Motion
- A thrown rubber ball re – bouncing from a wall.
- An athlete doing the high jump.
- A stone released from a catapult.
- A bullet fired from a gun.
- A thrown javelin
- A diver from a diving board.
- A shot arrow
The motion of a Projectile
Let us consider the simple case of a stone thrown horizontally with an initial velocity of u from the top of a high wall of height h. The stone is subject to two independent motions;
- A horizontal motion: once the stone is free and before it hits the ground and;
- A vertical motion: when the stone is initially thrown forward, the vertical pull of gravity will accelerate it downwards at a rate of about 9.8ms-1.
Any projectile in flight is doing two things at once; flying horizontally with a constant speed and moving up and down with an acceleration of g.
WORKED EXAMPLE
(1) A tennis ball is projected horizontally from the top of a vertical cliff 50m high with a velocity of 10ms-1.
Find:
(a) The time to reach the ground.
(b) The vertical component of the velocity when the ball hits the ground.
(c) The distance from the foot of the cliff where the ball hits the ground.
SOLUTION
(a) The ball falls vertically under the influence of gravity. Its vertical motion is independent of the horizontal motion.
Initial vertical velocity = 0, acceleration a = g, h = 50m
Recall from equations of motion, S = ut + ½at2
h = ut + ½gt2
50 = 0 + ½ x 10 x t2
50 = 5 t2
t2 = 10
t =![]()
t = 3.16s.
(b) Let v be the vertical component of the velocity when the stone hits the ground.
From equations of motion, v = u + at.
v = u + gt
v = 0 + 10 x 3.16
v = 31.6ms-1.
(c) Let s be the distance from the foot of the cliff where the ball hits the ground. The initial horizontal velocity is 10ms-1 and not affected by vertical acceleration therefore, a = 0.
From equations of motion, S = ut + ½at2
S = ut + 0 (since a = 0)
S = 10 x 3.16
S = 31.6m.
PATH OF A PROJECTILE
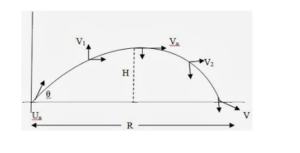
Vertical & horizontal components of velocity
When a particle is projected under gravity at a velocity u at an angle θ to the horizontal (neglecting air resistance) it follows the curve of a parabola.
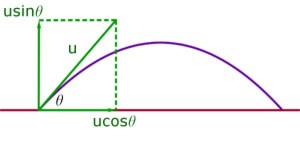
The particle has an initial horizontal speed of ucosθ, which is unchanged throughout the motion.
Vertically the particle has an initial speed of usinθ. It falls under gravity and is accelerated downwards with an acceleration of g ms-1, where g = 9.8 ms-2 (approx.)
NOTE
- The horizontal component of initial velocity = ucosθ.
- The vertical component of initial velocity = usinθ.
- The horizontal component of velocity (ucosθ) remains the same during the whole journey as no acceleration is acting horizontally.
- The vertical component of velocity (u sin θ) decreases gradually and becomes zero at the highest point of the path.
- At the highest point, the velocity of the body is u cos θ in the horizontal direction and the angle between the velocity and acceleration is 90°.
Time of flight
The time of flight is calculated from the vertical component of the velocity. It is the time it takes for the particle to go up, reach its maximum height and come down again. So this is twice the time to maximum height.
If the time to maximum height is t seconds. Then the time of flight is 2t.
Consider motion up to maximum height. This is attained when the final velocity v = 0.
Initial speed vertically upwards = usin
Using v = u + at
Replacing u by (usin)
Substituting for acceleration a = -g
When v = 0
0 = u sin θ – gt
t = u sin θ / g
Time of flight (2t) is
Maximum height attained (H)
The maximum height attained occurs when the particle is momentarily stationary, before falling under gravity. The vertical component of speed is zero at this point (v=0).
Using v2 = u2 + 2as
v2 – u2 = 2as
u is replaced with (u sin)
Distance s is height H
Substituting for acceleration a = – g
0 – u2 sin2 θ = – 2gH
– 2gH = – u2 sin2θ
H = u2 sin2θ / 2g
The Range (R)
The range is simply the horizontal component of speed multiplied by the time of flight.
The range of a projectile is given as:
The horizontal component x time to flight.
Using S = ut + ½at2
Since horizontal acceleration = 0
R = u cos θ x T
= u cos θ x 2u sinθ / g
Where T = 2u sinθ / g
R = 2u2cos θ sinθ / g
R = u2 sin2 θ / g
Recall for trigonometric function (2sinθ cosθ) = sin2
If sin 2maximum, then 2θ = 90°
Therefore θ = 45°
Maximum range is achieved in the horizontal when the angle, the projected object makes with the horizontal is 45°
Rmax = u2 / g
The above expression is the value of the Range of a projectile.
WORKED EXAMPLES
A projectile is fired with an initial velocity of 100ms-1 at an angle of 30° to the horizontal. Calculate:
(i) The time of flight.
(ii) The maximum height.
(iii) The range.
Solution
(i) T = 2u sinθ / g
T = 2 * 100 sin 30 / 10
T = 2 * 100 * 0.5 / 10
T = 10s
(ii) 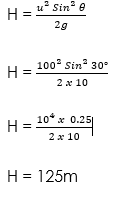
(iii) 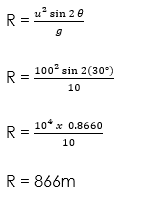
(2) A stone is thrown vertically upwards from the front with a velocity of 50m/s, Calculate:
(i) The maximum height reached
(ii) The time taken to reach the maximum height
(iii) The time of flight
SOLUTION
Given parameters:
Initial velocity, u = 50m/s
Acceleration g = – 10m/s2
Final velocity, v = 0
(i) 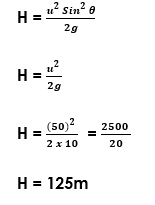
(ii) Time taken to reach max height
t = u/g = 50/10
t = 5 seconds
(iii) Time of flight
T = 2u/g = 2*50 / 10
T = 10 seconds
In our next class, we will be talking about the Equilibrium of Forces. We hope you enjoyed the class.
Should you have any further question, feel free to ask in the comment section below and trust us to respond as soon as possible.

Thanks ,
this note really helps
it was really helpful to me