Linear Momentum

Back to: PHYSICS SS2

Welcome to class! 

In today’s class, we will be talking about linear momentum. Enjoy the class!

Linear Momentum

Impulse

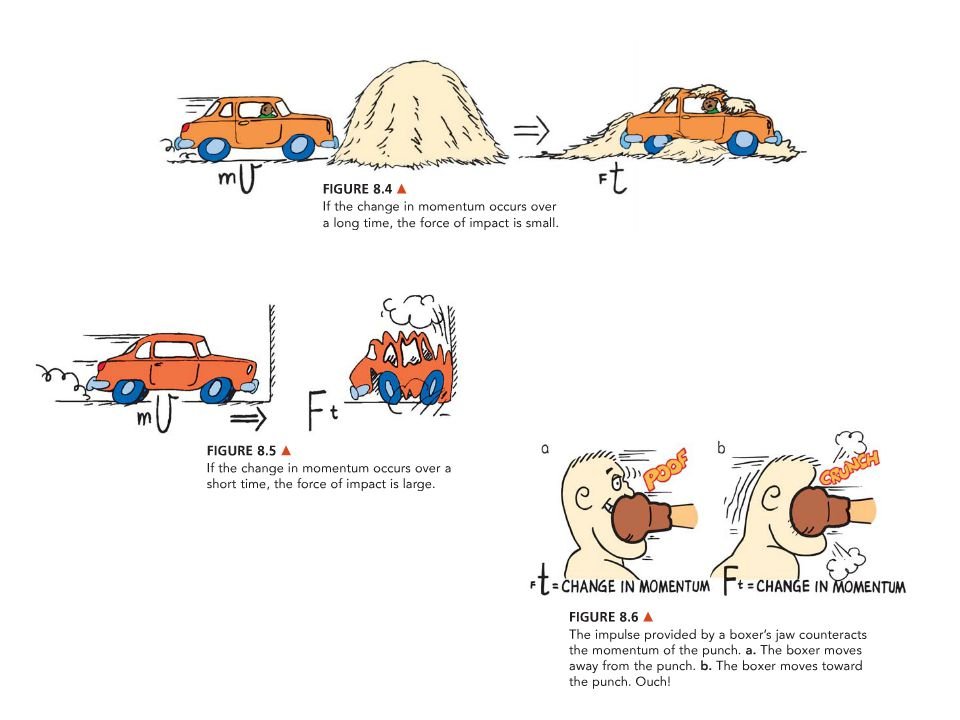
Impulse is also called blow. It is usually associated with a collision. It is a large changing force that acts for a short time. When an object collides with another object, each of them receives an impulse or a blow.

Impulse can also be defined as the product of the average force acting on a particle and the time during which the force act on the particle. The unit of impulse is Newton meter (Km).

Formula of Impulse

The formula for calculating impulse is as state below.
Impulse = force x time
I = F x t

Worked examples

(1) Calculate the impulse of a force of 240 N that act on 12 kg mass for 52½ minutes.

Solution
Data given in the question:
Mass = 12kg

Force = 240

Time = 52½ minutes

(Converting to seconds)

Time = (50 x 60 + ½ x 60)
Time = (3120 + 30) = 3150 seconds

Formula:                   impulse = Force x time
Substitution:           impulse = 240 x 3150 = 756000 Nm

(2) If a force of 25 N act on 5.25 kg mass and the impulse is 24.54Nm. Calculate the time for which the force acts on the object.

Solution
Data given in the question
Mass = 5.25 kg

Force = 25N

Impulse = 24.54Nm

Formula:                          Impulse = Force x time
Substitution:                    24.54 = 25 x time
Make time the subject:       Time =

$\frac{24.54}{25}$

Time = 0.981 second.

(3) The impulse of a force is 238 Nm. If the Force acts for 1235 seconds, calculate the magnitude of the force.

Solution
Data given in the question:
Impulse = 238 Nm, time = 1235 seconds, force = Unknown

Formula:                             Impulse = Force x time
Substitution:                       238 = Force x 1235
Make force the subject:    Force = 238 / 1235
Force = 0.192 Newton

Momentum

Momentum can be defined as the product of the mass of the object and its velocity. The unit of momentum is kilogram meter per second (Kg m/s). It is a vector quantity. The symbol that is used to represent momentum is P.

Formula of Momentum
The formula for calculating momentum is as stated below:
Momentum = mass of object x its velocity
P = m x v

Worked examples

(1) A car of mass 125 g moves with a velocity of 25m/s. Calculate the momentum of the car.

Solution
Data given in the question:
Mass = 125 g =   = 0.125 kg

Velocity = 25 m/s

Momentum = Unknown

Formula:                                Momentum = mass x velocity
Substitution:                          Momentum = 0.125 x 25
Momentum = 3.125Nm

NEWTON’S LAWS OF MOTION

The motion of objects is caused by unbalanced forces that act on the objects. Therefore, forces are related to the motions of objects. This was discovered by Sir Isaac Newton (1642 – 1727). He stated three laws of motion which we shall look into in the treatment.

NEWTON’S FIRST LAW OF MOTION

Newton’s first law of motion states that an object will continue in its state of rest or motion in a straight line unless it is acted upon by an external force.

• Inertia
  Inertia is the unwillingness of an object in motion to stop moving or an object at rest to start moving. Inertia simply means unwillingness.
• Mass
  Mass is the quantity of matter that is contained in an object. The more the quantity of matter that is contained in an object, the larger the mass of the object. Mass is measured in kilogram (kg). It is a scalar quantity.
• Inertial Mass
  Inertial mass is a property of a matter which represent a resistance that the resistance f the object to any type of force.
• Weight
  Weight of an object is the gravitational pull on the object or It can be defined as the force that is acting on the object due to the earth gravitational pull. Weight is measured in Newton. It is a vector quantity.

Relationship between Mass and Weight

This formula is used in calculations, to either calculate the weight of a given mass of an object or to calculate the mass of a given weight.

The formula is:        Weight = mass x acceleration due to gravity
Weight = m x g

Worked examples

(1) Calculate the weight of a mass 2.6gram.

Solution
Data given in the question:
Mass = 225g =  = 0.225 kg.
Formula:            Weight = mass x acceleration due to gravity
Substitution:      Weight = 0.225 x 10.

Weight = 2.25 N

(2) What is the mass of an object whose weight is 35N? (g = 10 m/s²)

Solution
Data given in the question:
Weight = 35 N, g = 10 m/s²
Formula:             weight = mass x acceleration due to gravity
Substitution:       35 = mass x 10
Make mass the subject:    Mass =

Mass = 3.5 kg 

Significance of Newton’s First Law of Motion

The significance of Newton’s first law of motion is that Newton’s first law of motion makes us understand that inertia (unwillingness) is present in every object.

Short Coming of Newton’s First Law of Motion

Newton’s first law of motion does not suggest how force should be measured.

NEWTON’S SECOND LAW OF MOTION

Newton’s second law of motion states that the rate of change of momentum is directly proportional to the force that caused the change and take place in the direction of the force.

Relationship between Force and Mass

Force = mass of object x acceleration of the object
F = m x a

Worked examples

(1) Calculate the magnitude of the force that acts on 12kg mass such that its acceleration is 1.75 m/s².

Solution
Data given in the question:
Mass = 12kg, acceleration = 1.75 m/s², Force = Unknown

Formula:                                Force = mass x acceleration
Substitution:                          Force = 12 x 1.75
Force = 21N

The formula for Newton’s Second Law of Motion

Newton’s second law of motion is obtained as follow:
Mathematically,
Force is directly proportional to the rate of change in momentum

$$\begin{gathered} Force \propto rate of change in momentum \\ Force \propto \frac{Change in Momentum}{time taken} \\ Force \propto \frac{mv – mu}{time} \\ Factorize m: Force \propto \frac{m(v–u)}{t} \\ Recall that acceleration a = \frac{Final velocity\left(v\right) – Initial velocity\left(u\right)}{time \left(t\right)} \\ a = \frac{v – u}{t} \\ Hence, \\ Force \propto mass \times acceleration \\ Force \propto m\times a \\ Force = k \times m\times a \\ If cons\tan t k is 1, then the formula will become, \\ Force = mass \times acceleration \\ Or: Acceleration = \frac{Force}{mass} \\ Or: Mass = \frac{Force}{acceleration} \end{gathered}$$

Worked examples

(1) A ball of mass 3 kg that is moving with a velocity of 26m/s is suddenly hit by a Force of 6N for 0.05 second. Find the new velocity of the object.
Solution
Data given in the question:
Mass = 3 kg

Velocity =26 m/s

Force = 6N

Time = 0.05 second

NEWTON’S THIRD LAW OF MOTION

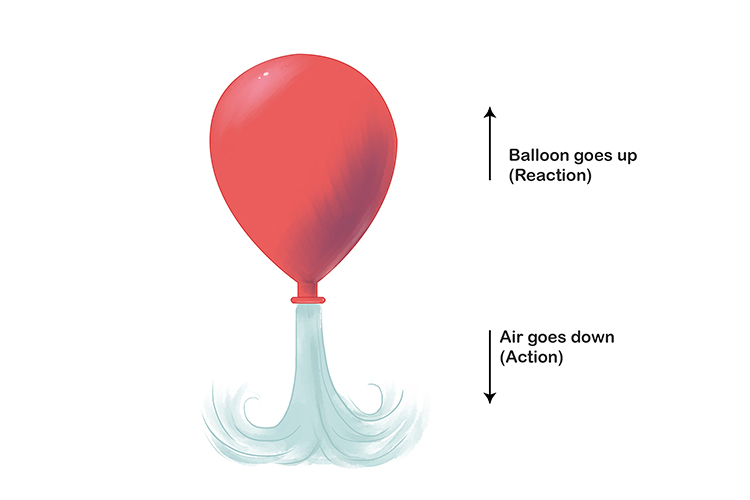
Newton’s third law of motion states that to every action, there is an equal and opposite reaction

Action = – Reaction.

Explanation Of Newton’s Third Law Of Motion:

Newton’s third law of motion says that if object A hits another object B with a force F_a, then object B in turn also hit object A with the same amount of force as F_a.
Force F_a of object A = force F_b of object B but in the opposite direction.
Therefore,
F_a = – F_b

EVALUATION

1. An unbalanced force of 25 N acts on 8.0 kg mass. What does it give to the mass?
2. An object of mass 950g is pulled along a tarmac by a horizontal force of 20 N. A frictional force of 6 N opposed the motion. What is e acceleration of the stone?

 

In our next class, we will be talking about the Principle of Conservation.  We hope you enjoyed the class.

Should you have any further question, feel free to ask in the comment section below and trust us to respond as soon as possible.

Get more class notes, videos, homework help, exam practice on Android [DOWNLOAD]

Get more class notes, videos, homework help, exam practice on iPhone [DOWNLOAD]