Back to: PHYSICS SS2
Welcome to class!
In today’s class, we will be talking about gas laws. Enjoy the class!
Gas Laws

Gas laws are the laws that explain the relationships between the pressure, volume and temperature of gas. The laws show and explain how each of the gas property behaves when there is a change in any of the properties.
The gas laws are very important formulae for solving gas related problems.
BOYLE’S LAW
Boyle’s law gives the relationship between the pressure of a gas and volume of the gas at a constant temperature. Basically, the volume of a given mass of gas is inversely proportional to the pressure of gas provided that temperature is kept constant.

Boyle’s law equation is written as:
V ∝ or P ∝ or PV = k1
Where V is the volume of the gas, P is the pressure of the gas and K1 is the constant. Boyle’s Law can be used to determine the current pressure or volume of gas and can be represented also as;
P1V1 = P2V2
WORKED EXAMPLES
(1) 18.10mL sample of gas is at 3.500 atm. What will be the volume if the pressure becomes 2.500 atm, with a fixed amount of gas and temperature?
Solution
Given parameters:
P1 = 3.500atm
V1 = 18.10mL
P2 = 2.500atm
V2 = Unknown

CHARLES LAW
Charles law states that at constant pressure, the volume of a gas is directly proportional to the temperature (in Kelvin) in a closed system. Basically, this law describes the relationship between the temperature and volume of the gas.

Mathematically, Charles’s law can be expressed as;
V ∝ T
Where;
V = volume of gas,
T = temperature of the gas in Kelvin.
Another form of this equation can be written as;
![]()
Charles’s law problem
A sample of Carbon dioxide in a pump has a volume of 21.5mL and it is at 50.0oC. When the amount of gas and pressure remain constant, find the new volume of Carbon dioxide in the pump if the temperature is increased to 75.0oC.
Solution
Given parameters:

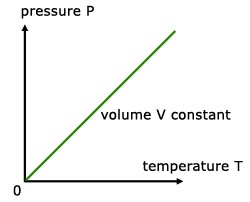
PRESSURE LAW
For a fixed mass of gas at constant temperature and pressure, the pressure is directly proportional to the temperature (K).

Measurement of gas Pressure
The manometer is the instrument that is used to measure gas pressure. It consists of a u-tube that contains either water or mercury.
How to Use a manometer
One end of the u-tube that contains mercury or water is opened to the atmosphere while the other end is connected to a gas supply
Diagram of manometer



The free arm of the manometer is raised or lower until the mercury levels in both arms of the tube are at the same level. The gas supply is then opened to allow gas into the manometer. The gas pressure on the mercury level in the left arm of the tube forces the mercury level in the right arm of the tube to rise up a certain height above that in the left arm of the tube. The difference in the height h between the mercury levels in both arm of the tube is determined.
Formula for Calculation
From figure I,
When mercury level X is below level above Y,
Draw a horizontal line from level x at the left arm of the u-tube to cut the right arm of the u-tube and mark that point as y.
Theory of calculation:
The pressure at x = pressure at y
The pressure at x is the pressure from the gas
The pressure at x = gas pressure.
The pressure at y is the atmospheric pressure that is acting on the mercury level at the open end of the u-tube and the pressure due to the height of the mercury column, h.
Therefore,
The pressure at y = atmospheric pressure + pressure due to h
The pressure at y = Atm. Pressure + h
Now;
The pressure at x = pressure at Y
gas pressure = atmospheric pressure + pressure due to h
gas pressure = Atm. Pressure + h
At this point, if the atmospheric pressure is known and the pressure produced by h is also known, you can calculate the gas pressure by adding the two.
You must know that in some questions, you may be required to calculate the pressure produced by the liquid column h. In such questions, you would be given the data you heeded for the calculation of the pressure produced by liquid column h.
Note:
The formula for calculating the pressure of a liquid column of height h.
Pressure in liquid = height x density x acceleration due to gravity
Pressure of liquid = h x ρ x g
From figure II,
In figure II, the mercury levels in both arms of the u-tube are at the same level. In this case, h = 0. Therefore, it is only atmospheric pressure that is acting at point Y. Going by the theory of calculation, we will get,
Theory of calculation:
The pressure at x = pressure at y
The pressure at x is the pressure from the gas.
The pressure at x = gas pressure.
The pressure at y is the atmospheric pressure that is acting on the mercury surface at y. there is no pressure due to h because h is zero.
Therefore,
The pressure at y = atmospheric pressure.
Theory of calculation:
The pressure at x = pressure at y
Gas pressure = atmospheric pressure
From figure III
In figure III, the mercury level in the right arm of the u-tube is below the mercury level in the left arm of the u-tube.
Theory of calculation:
The pressure at x = pressure at y
The pressure at x = gas pressure + pressure due to height of mercury column h
Pressure at x = gas pressure + h
The pressure at y = atmospheric pressure.
Therefore,
gas pressure + h = atmospheric pressure
gas pressure + h = atm. Pr
You make gas pressure the subject of the formula:
gas pressure = Atm. Pressure – h
THE GENERAL GAS LAW
The General Gas Law is an equation obtained as a result of the combinations of Charles’ law, Boyle’s law and Pressure law.
Boyle’s law = PV = K where K is constant
Charles’ law = V/T = K
Pressure law = P/T = K

The general relationship between pressure, volume and temperature of a given mass of gas is called the equation of state or ideal gas law or general gas law.
Application of Gas-law
- During summer when the temperature is high and pressure is also high, a tire is at risk of bursting because it is inflated with air.
- The law is also used often in thermodynamics as well as in fluid dynamics.
- It can be used in the weather forecast systems.
WORKED EXAMPLES
(1) What length of the column of a barometer tube would support an atmospheric pressure of 10200Nm-2 if the density of the liquid is 2600kgm-3? [g =10m/s2]
SOLUTION
Pressure P of the liquid column h in a barometer is given by:
P = hρh
10200 = h x 2600 x 10
h = 3.92 m
We hope you enjoyed the class.
Should you haveany further question, feel free to ask in the comment section below and trust us to respond as soon as possible.
School Owner? Looking for ready-made content and tools to save time and grow easily? Book a free demo session nowGet more class notes, videos, homework help, exam practice on Android [DOWNLOAD]
Get more class notes, videos, homework help, exam practice on iPhone [DOWNLOAD]