Equilibrium of Bodies in Liquid

Back to: PHYSICS SS2

 

Welcome to class! 

In today’s class, we will be talking about the equilibrium of bodies in liquid. Enjoy the class!

Equilibrium of Bodies in Liquid

When a heavy object is immersed in a liquid the object appears to become lighter. Consider the experience when a bucket of water is being drawn out of a well. While still under the water the bucket appears very light and becomes very heavy as soon as it is out of water.

Archimedes explains this showing that when the bucket still in the water, the body is acted upon by an upward force U called upthrust. While still underwater, the equilibrium of the bucket is as: T = W – U.

Where T = tension in the rope.

W = weight.

U = upthrust.

U = W – T. It is also known as loss in weight.

ARCHIMEDES PRINCIPLE

It states that when an object is wholly or partially immersed in a fluid, it experiences a loss in weight or an upthrust which is equal to the weight of the fluid displaced by the object.

FLOATING

If a body is denser than the liquid, it will completely sink in it, but if the density of the body is less than that of the liquid, the body sinks until the weight of the liquid displaced is just equal to the weight of the body. The body then floats and is said to be in equilibrium. This is the condition necessary for a body to float.

PRINCIPLE OF FLOATING

It states that a floating body displaces its own weight of the liquid in which it floats or a body floats when the upthrust exerted upon it by the fluid is equal to the weight of the body.

IMPORTANCE OF FLOATING PRINCIPLE

Ships float in water even though they are made of steel which is denser than water. This is because they are hollow objects containing a large amount of air and so able to displace a large amount of water, given an upthrust large enough to support the weight of the ship. Likewise, the weight of a balloon and its content is equal to the upthrust of air on the balloon.

WORKED EXAMPLE

(1) An object weighs 0.08N in air and 0.01N in a liquid of density 700kgm^-3. Calculate the upthrust of the liquid on the solid.

SOLUTION

Since upthrust = loss in weight

Upthrust is given as (0.08 – 0.01) N = 0.07N.

DENSITY AND UPTHRUST

The density of a substance is its mass per unit volume.

Density = mass/volume

          ρ =m/v

Where ρ(rho) is a Greek letter representing density. Its S.I. unit is kgm^-3.

WORKED EXAMPLE

(1) An object weighs 0.08N in air and 0.01 N in a liquid of density 700kgm^-3. Calculate the volume of the solid.

SOLUTION

ρ =mass/-volume

v =mass/-density

For density,

700kgm^-3  =  0.7gcm^-3

For mass,

0.007kg = 0.007 x 1000 = 7g

v = 7/-0.7 = 10cm³

RELATIVE DENSITY (R.D)

Since water is the most common substance and its density is 1000kgm-3 or 1gcm-3, it is convenient to use it as a standard for comparing the densities of other substances.

The relative density (R.D) of a substance is defined as follows:

R.D = relative density of substance/density of water

= mass of substance/mass of an equal volume of water

= weight of substance/weight of an equal volume of water

Relative Density has no unit.

DETERMINATION OF R.D

1. Regular body: For a regular body, the volume can easily be found and the mass can be obtained by direct weighing. Hence density can be calculated.
2. Irregular body: The mass can be obtained by direct weighing. The volume is found by immersing the body in water provided it will not dissolve in water and it will sink. The volume of water displaced will equal the volume of the solid. Hence, the density can be calculated.

RELATIVE DENSITY OF LIQUID BY DIRECT METHOD

A relative bottle can be used to find the density of a liquid directly.

The relative bottle is weighed empty and has a mass of m. It is then filled with liquid and weighed and has mass m₁. Finally, it is emptied, dried and refilled with water and weighed again when it has mass m₂.

Recall that Relative density =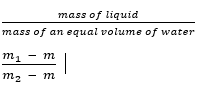

The relative density of a solid in the form of a powder (sand or steel ball-bearing)

The density bottle is weighed empty (m₁) and again weighed when about one – third full of sand (m₂). The bottle with sand is filled up with water and reweighed (m₃). Finally, the bottle is emptied of its content, filled full of water, and weighed (m₄).

The relative density of the sand is obtained as follows:

R.D =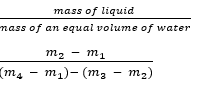

The instrument used for measuring density

1. A hydrometer is an instrument for measuring the density of liquids. Its construction and operation are based on the fact that the depth to which a tube sinks depends on the density of the liquid in which it is floating.
2. A practical hydrometer is an instrument which gives a direct density reading of the liquid in which it floats. It works from the principle that less the density of the liquid, further the hydrometer sinks into it.

This shows that l α ¹/_ρ.

 

In our next class, we will be talking about Introduction to Simple Harmonic Motion (SHM).  We hope you enjoyed the class.

Should you have any further question, feel free to ask in the comment section below and trust us to respond as soon as possible.

School Owner? Looking for ready-made content and tools to save time and grow easily? Book a free demo session now

Get more class notes, videos, homework help, exam practice on Android [DOWNLOAD]

Get more class notes, videos, homework help, exam practice on iPhone [DOWNLOAD]