Back to: PHYSICS SS2
Welcome to class!
In today’s class, we will be talking about the principle of conservation. Enjoy the class!
Principle of Conservation

Principle of conservation of linear momentum states that if two or more bodies in a closed or isolated system collide, their total momentum before the collision is equal to their total momentum after the collision.
In a closed system,
Momentum before collision = momentum after collision.
(Mass x velocity) before collision = (Mass x velocity) after collision
Note that the principle of the conservation law of linear momentum emanates from Newton’s second and third law of motion.
A Closed/Isolated System
A closed or isolated system means a system on which no external force act.
Types Of Collision
There are two types of collisions: elastic collision and inelastic collision.
- Elastic collision: Elastic collision is the type of collision whereby the colliding objects bounce back with the same amount of velocity or different amount of velocities. The colliding objects do not stick together. In an elastic collision, both kinetic energy and momentum are conserved.
Examples of Elastic Collision
- The collision of the ball and a wall
- The collision of gas molecules
- Inelastic Collision: Inelastic collision is the type of collision whereby the colliding objects stick together and move with a common velocity v. In inelastic collision, only momentum that is conserved. Kinetic energy is a loss because the kinetic energy is converted into sound energy, heat energy.
Different Cases of Collision
(1) When A Moving Object Collides With A Stationary Object, Stick Together and Move With Common Velocity, V:

The figure above represents a collision type whereby an object of M1 that is moving with initial U1 collides with a stationary object of mass M2. They stick together and move with a common velocity V.
Momentum:
Form the conservation law of momentum:
Momentum of the two objects before collision:
= Momentum of M1 + Momentum of M2
= M1 x U1 + M2 x U2
Momentum of the two objects after collision:
= Momentum of M1 + Momentum of M2
= M1 x V + M2 x V = V(M1 + M2)
Combining momentum:
Momentum of objects before collision = Momentum of objects after collision
M1 x U1 + M2 x U2 = V(M1 + M2)
(Recall) U2 = 0 m/s (the is at rest)
M1 x U1 + M2 x 0 = V(M1 + M2)
M1 x U1 + 0 = V(M1 + M2)
![]()
Kinetic Energy:
Kinetic energy of the two objects before collision = K.E of M1 + K.E of M2
= ½ x (M1) x (U1)² + ½ x (M2) x (U2)²
Also,
Kinetic energy of the two objects after collision = K.E of M1 + K.E of M2
=½ x (M1) x (V)² + ½ x (M2) x (V)²
Total Kinetic before collision = Total kinetic energy after collision
½ x (M1) x (U1)² + ½ x (M2) x (U2)² = ½ x (M1) x (V)² + ½ x (M2) x (V)²
Since M2 is stationary, U2 = 0 m/s. Then
½ x (M1) x (U1)² + ½ x (M2) x (0)² = ½ x (M1) x (V)² + ½ x (M2) x (V)²
½ x (M1) x (U1)² + 0 = ½ x (M1) x (V)² + ½ x (M2) x (V)²
½ x (M1) x (U1)² = ½ x (M1) x (V)² + ½ x (M2) x (V)²
½ x (M1) x (U1)² = ½(M1 + M2)V²
½ in both sides cancels one another
(M1) x (U1)² = (M1 + M2)V²
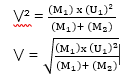
Loss in Kinetic Energy:
Loss in kinetic energy can be calculated as follows:
•Calculate the kinetic energy of the two objects before collision
•Calculate the kinetic energy of the two objects after collision
•Then find the difference between the two kinetic energy to get the kinetic energy loss.
Therefore,
Kinetic energy loss = K.E before the collision – K.E after collision
K.E of the two objects before collision = ½ x (M1) x (U1)²
Also,
K.E of the two objects after collision = ½(M1 + M2)V²
Kinetic energy loss = K.E before the collision – K.E after collision
(2) When A Moving Object Collides With A Stationary Object and They Move In The Same Direction With Different Velocities:
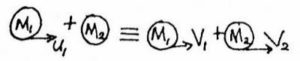
From the figure above, the object of mass M1 moving with initial velocity U1 collides with a stationary object of mass M2 and the two moves with a different final, V1 and V2.
Momentum:
Form the conservation law of momentum:
The momentum of objects before collision = momentum of objects after the collision
M1 x U1 = (M1V1+ M2V2)
Kinetic Energy:
Total Kinetic before collision = Total kinetic energy after collision
½ x (M1) x (U1)² = ½ x (M1) x (V1)² + ½ x (M2) x (V2)²
(M1) x (U1)² = (M1) x (V1)² + (M2) x (V2)²
How To Calculate Loss in Kinetic Energy:
Kinetic energy loss = K.E before the collision – K.E after collision
Loss in kinetic energy = ½ x (M1) x (U1)² – ½ x [(M1) x (V1)² + (M2) x (V2)²]
(3) When Two Objects That Move In The Same Direction Collide, Stick Together And Move With A Common Velocity:
Momentum:
Total momentum before collision = Total momentum after the collision
M1 x U1 + M2 x U2 = M1 x V1 + M2 x V2
M1 x U1 – M1 x V1 = M2 x V2
![]()
Kinetic Energy:
Total Kinetic before collision = Total kinetic energy after the collision
½ x (M1) x (U1)² + ½ x (M2) x (U2)² = ½ x (M1) x (V)² + ½ x (M2) x (V)²
[(M1) x (U1)² + (M2) x (U2)²] = (M1 + M2) V²
![]()
How To Calculate Loss in Kinetic Energy:
Loss in kinetic energy can be calculated as follows:
Kinetic energy loss = K.E before the collision – K.E after collision
Loss in kinetic energy = ½ x M1 x (U1)² – ½ x (M1 x (V1)² + M2 x (V2)²)
Application Of Newton’s Law And Conservation Law Of Momentum
The principle of conservation of linear momentum is applied in the following which we will discuss below:
(1) Recoil Of A Gun:
When a gun is fired, the bullet is energized by a forward force (action) which moves it forward with a certain velocity. The bullet has a forward momentum while the gun has a backward momentum which is equal in magnitude to the forward momentum of the fired bullet.
Let,
Mg be mass of the gun
VG be the velocity of the gun
Mb be mass of the bullet
Vg be the velocity of the bullet
Then,
Momentum of gun = Mg x Vg
Momentum of bullet = Mb x Vb
By the principle of the law of conservation of linear momentum:
The forward momentum of Bullet = Backward momentum of the gun
Therefore,
Mb x Vb = Mg x Vg
2. Jet and Rocket Propulsion:
The principle of conservation of linear momentum is also utilized in the propulsion of jet, aircraft and rockets.
3. Why Walking Is Possible
Weight of an Object Inside A Lift
When a man stand in a lift or elevator, two forces act on the man. The forces are:
(i) The true weight of the man which act vertically downward (w = m x g)
(ii) The reaction force R of the floor of the lift on the man, which act upward.
We are going to look into different cases when the man is on the lift
Weightlessness In Satellites:
People and object is a satellite that is orbiting close to the earth experience weightlessness.
In our next class, we will be talking about Mechanical Energy. We hope you enjoyed the class.
Should you have any further question, feel free to ask in the comment section below and trust us to respond as soon as possible.

I noticed that your unit of impulse is Nm. I know it to be Ns since the formula is force× time. Also that of momentum is kgm/ s. not Nm. Thanks