Equations of Motion

Back to: PHYSICS SS2

Welcome to class!

In today’s class, we will be talking about Equations of Motion. Enjoy the class!

Recall the four equations of motions as derived in the previous class:

v = u + at
v² = u² + 2as
S or h = ut + ½at²
S = (u+ v)/2 x t

DERIVATION OF EQUATION 1

Equation 1 is derived from the formula of acceleration. The derivation is as follows:

Acceleration = change in velocity/time

Acceleration a = final velocity(v) – initial velocity(u)/time

Using their symbols, the formula will become:

A = v – u/t

Make v the subject of the formula.

A x t = v-u

V = u + at which is the equation 1.

DERIVATION OF EQUATION 2

To obtain equation 2, we will use the formula for average velocity and substitute for v = u + at in the formula of average velocity as follows:

Average velocity:

V_average = (u + v) / 2

At this point, you substitute for v; when v = u + at.

Therefore,

V_average = (u + v) / 2

V_average= (u + u + at) / 2

V_average = (2u + at) / 2 ….. Equation (1)

At this point, you open the bracket:

V_average = u+½at

Also, the formula for average velocity is,

V_average = distance(s)/time(t)

V_average= s/t ……………… Equation 2

You equate the two equations as follows:

Equation 1 = Equation 2

V_average of equation 1 = V_average of equation 2

u + ½at =

You make s the subject by cross multiplying t.

(u + ½at) x t = s

ut + ½at x t = s

ut + ½at² = s

s = ut+½at² …….… Equation 2

DERIVATION OF EQUATION 3

Equation 3 can be obtained by squaring both sides of equation 1.

Therefore,

v² = (u+at)²

v² = (u+at) x (u+at)

v² = u² + 2uat + a²t²

v² = u²+2uat + (at)²

At this point, you factorize 2a from 2uat+(at)².

Therefore, you will get,

v² = u² + 2a (ut+½(at)² ……………… (i)

At this point, you have to recall that,

s = ut+½at²

You will have to substitute s for ut+½at² in equation (i)

Therefore;

v² = u² + 2a (ut+½(at)²

v² = u²+2as which gives equation 3.

DERIVATION OF EQUATION 4

Equation 4 is obtained by equating the two formulae of average velocity.

The two formulae for average velocity are:

V_{average (1)}= s/t

V_{average (2)} = (u + v)/2

Therefore,

V_{average (1)} = V_{average (2)}

s/t = (u + v)/2

You make s the subject of the formula:

s = (u + v)/2 x t which gives equation 4.

APPLICATION OF EQUATIONS OF MOTIONS

WORKED EXAMPLES

(1) A stone is thrown vertically upward from the ground with a velocity of 20m/s.

(g = 10 m/s²). Calculate:

(i) The maximum height reached.

(ii) The time to reach the maximum height;

(iii) The time to reach the ground again;

(iv) The velocity reached halfway up.

SOLUTIONS

Recall the steps as stated in the previous class.

Recall that at maximum height, v = 0m/s

Data given in the question:

U = 20m/s; v = 0m/s; g = 10m/s².

(i) Maximum height reached:

Formula:

v² = u²+2as

Substitution:

0² = 20² + 2 x (-10) x s

0 = 400 + (-20s)

0 = 400 – 20s

Collect like terms and make s the subject of the formula.

20s = 400

S =

The maximum height reached = 20m.

(ii) The time taken to reach maximum height:

Formula:

s = ut+½at²

Substitution:

20 = 20 x t + ½ x (-10) x t²

20 = 20t – 5t²

You rearrange the quadratic equation and find t using any formula that is convenient with you.

Therefore,

0 = 20t – 5t² – 20

0 = -5t² + 20t – 20

You now factorise or use the general formula to find t.

Using the general formula:

Where,

a = – 5; b = 20; c -20

Substitution:

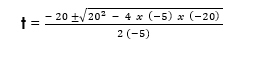
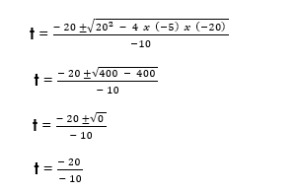
Time to reach maximum height (t) = 2s

(iii) The time to reach the ground again:

The time to reach the ground is the same as the time taken to reach maximum height.

Therefore,

Time to reach ground = 2 x time taken to reach maximum height.

Time to reach ground = 2 x 2s

Time to reach ground = 4s.

(iv) The velocity reached halfway up:

To calculate the velocity of the object halfway up, the time taken to travelled half distance is half of the time taken to reached maximum height. Or you use half the distance travelled to calculate its velocity halfway up.

Therefore,

The distance half way up = = 10m

Formula:

v² = u²+2as

Substitution:

v² = 20² + 2 x (-10) x 10

v² = 400 – 200

v² = 200;

v =

Velocity half way = 14.14m/s

(2) A train travelling at 54km/h accelerates uniformly at 3m/s² for ¼ minutes. Calculate:

(i) The distance travelled in this time.

Solution:

Data given in the question:

u = 54km/h (recall the conversion technique in previous class

u = = 15m/s (v = 15m/s);

a = 3m/s²;

Time (t) = ¼ min = ¼ x 60 = 12sec;

Formula:

s = ut + ½at²

Substitution:

s = 15 x 12 + ½ x 3 x 15²

s = 180 + ½ x 3 x 225

s = 180 + 337.5

s = 517.5m

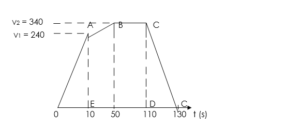
(3) A body at rest is given an initial uniform acceleration of 8.0m/s² for 30s after which the acceleration is reduced to 5.0m/s2 for the next 20s. The body maintains the speed attained for 60s after which it is brought to rest in 20s. Draw the velocity-time graph of the motion using the information given above:

(b) Using the graph, calculate the:

(i) Maximum speed attained during the motion

(ii) Average retardation as the body is being brought to rest

(iii) Total distance travelled during the first 50s

(iv) Average speed during the same interval as in (iii)

SOLUTION

(a) Graph:

Note: Velocity is not given in the equation, so we will need to convert first.

After 30s the velocity v₁ gained

Whenever a body is at rest initial velocity is zero

v₁ = u + at

v₁ = 0 + 8 x 30

v₁ = 240m/s (v₁ = u)

This enables the point A to be plotted, so that OA is the part of the graph showing the uniform acceleration. Also change in velocity after 20s,

v₂ = u + at

v₂ = 240 + 5 x 20

v₂ = 240 + 100

v₂ = 340m/s.

Thus draw the line AB so that AB or EF represents 20s. Now draw the line BC parallel to the time-axis so that BC or FG represents 60s.

Finally, join C to D, which is 20s further than G on the time-axis.

(b) (i)v/30 = 8

v₁ = 30 x 8

v₁ = 240 m/s

Also change in velocity after 5s

= 5

v₂ – v₁ = 100

v₂ = v₁ + 100

v₂ = 240 + 100

v₂ = v_max = 340m/s

(ii) Average retardation along CD = slope of IV

= change in velocity / time

CG/GD = 340m/s / 20s

= 17m/s²

(iii) Total distance for first 50s

= area of triangle OAE x area of trapezium EABF

= ½ OE x AE + ½ (AE + BF) x EF

= ½ (30) x 240 + ½ (240 + 340) x 20

= (3600 + 5800) m

= 9400 m

In our next class, we will be talking about Projectiles. We hope you enjoyed the class.

Should you have any further question, feel free to ask in the comment section below and trust us to respond as soon as possible.

Access more class notes, videos, homework help, exam practice on our app HERE

Boost your teaching with ready-made, downloadable class notes and more on our app HERE!

Equations of Motion