Introduction to Simple Harmonic Motion (SHM)

Back to: PHYSICS SS2

 

Welcome to class! 

In today’s class, we will be talking about the introduction to simple harmonic motion (SHM). Enjoy the class!

Introduction to Simple Harmonic Motion (SHM)

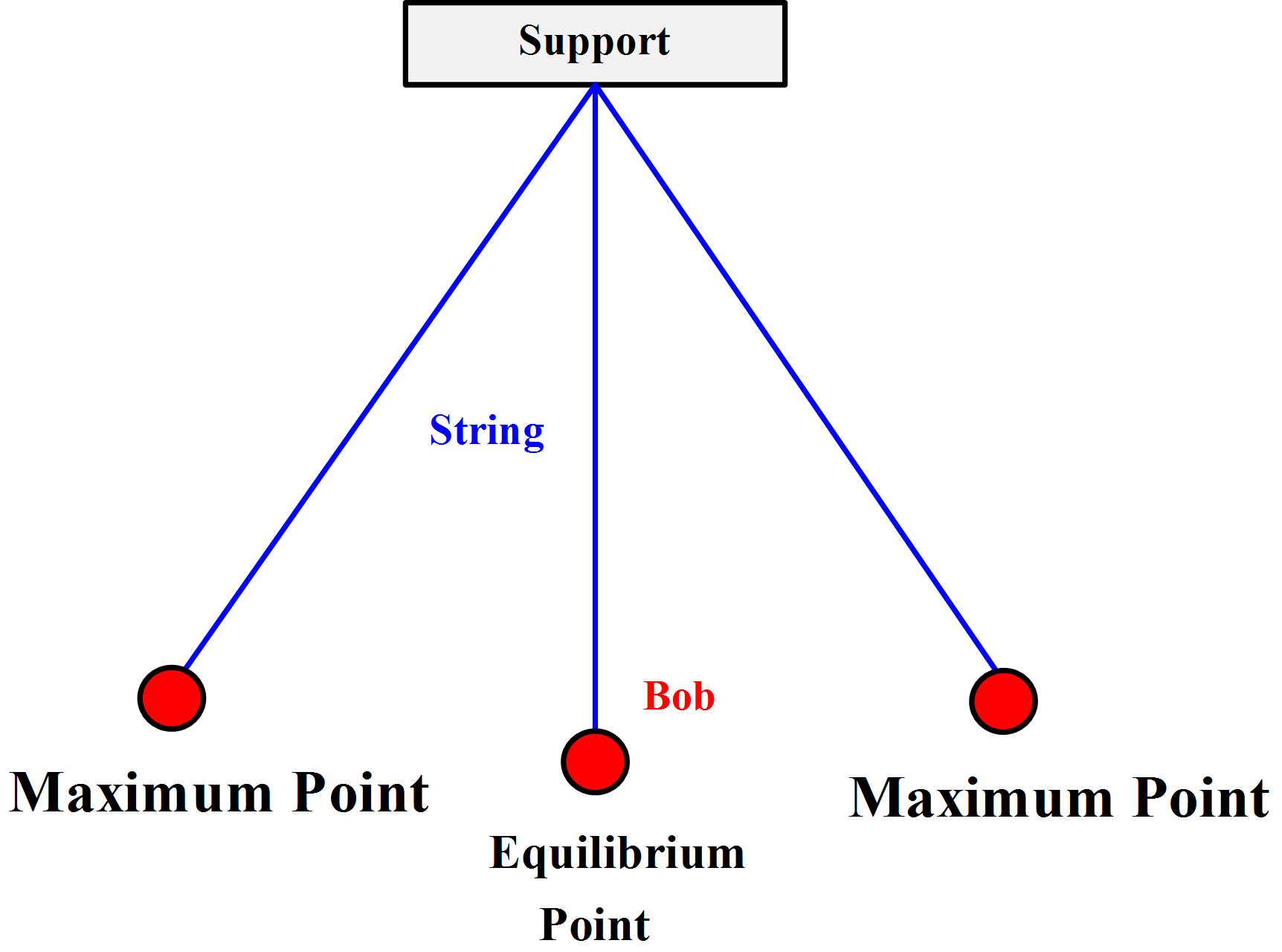
Simple Harmonic, Periodic and Oscillation Motion

Simple harmonic motion can be described as an oscillatory motion in which the acceleration of the particle at any position is directly proportional to the displacement from the mean position. It is a special case of oscillatory motion.

In this type of oscillatory motion displacement, velocity and acceleration and force vary in a way that can be described by either sine (or) the cosine functions collectively called sinusoids.

The study of Simple Harmonic Motion is very useful and forms an important tool in understanding the characteristics of sound waves, light waves and alternating currents. Any oscillatory motion which is not simple Harmonic can be expressed as a superposition of several harmonic motions of different frequencies.

Difference between Periodic, Oscillation and Simple Harmonic Motion

• Periodic Motion

1. A motion repeats itself after an equal interval of time. For example, uniform circular motion.
2. There is no equilibrium position.
3. There is no restoring force.
4. There is no stable equilibrium position.

• Oscillation Motion

1. To and fro motion of a particle about a mean position is called an oscillatory motion in which a particle moves on either side of equilibrium.
2. It is a kind of periodic motion bounded between two extreme points. For example, Oscillation of Simple Pendulum, Spring-Mass System.
3. In an oscillatory motion, the net force on the particle is zero at the mean position.
4. The mean position is a stable equilibrium position.

• Simple Harmonic Motion or SHM

1. It is a special case of oscillation along with straight line between the two extreme points (the path of SHM is a constraint)
2. Path of the object needs to be a straight line
3. There will be a restoring force directed towards equilibrium position (or) mean position
4. Mean position in Simple harmonic motion is a stable equilibrium.

SPEED AND ACCELERATION OF A SIMPLE HARMONIC MOTION

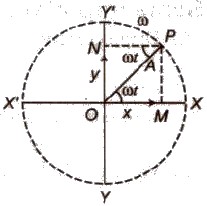
Non-harmonic Oscillation

A non-harmonic oscillation is a combination of two or more than two harmonic oscillations.

It can be expressed as y = a sin ωt + b sin 2ωt

Some Terms Related to SHM

(i) Time Period Time taken by the body to complete one oscillation is known as time period. It is denoted by T. (Period = T = ). S.I unit is second

(ii) Frequency The number of oscillations completed by the body in one second is called frequency. It is denoted by v.

Its S.I unit is ‘hertz’ or ‘second^-1‘.

(iii) Angular Frequency The product of frequency with factor 2π is called angular frequency. It is denoted by ω.

Angular frequency (ω) = 2πv

Its SI unit is ‘hertz’ or ‘second^-1‘.

(iv) Displacement A physical quantity which changes uniformly with time in a periodic motion. is called displacement. It is denoted by y.

(v) Amplitude The maximum displacement in any direction from the mean position is called amplitude. It is denoted by a.

(vi) Phase A physical quantity which expresses the position and direction of motion of an oscillating particle, is called phase. It is denoted by φ.

Some Important Formulae of SHM

(i) Displacement in SHM at any instant is given by

y = a sin ωt

or y = a cos ωt

where a = amplitude and

ω = angular frequency.

(ii) Velocity of a particle executing SHM at any instant is given by

v = ω

At mean position y = 0 and v is maximum

v_max = aω

At extreme position y = a and v is zero.

(iii) Acceleration of a particle executing SHM at any instant is given by

A or α = – ω² y

(-ve) indicates that the direction of acceleration is opposite to the direction in which displacement increases, i.e., towards mean position.

At mean position y = 0 and acceleration is also zero.

At extreme position y = a and acceleration is maximum

a_max = – aω²

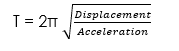
(iv) Time period in SHM is given by

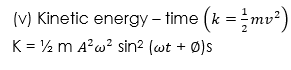
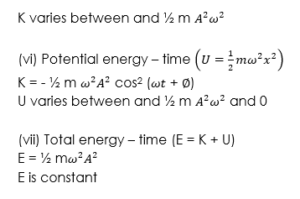
WORKED EXAMPLES

(1) A simple pendulum has a period of 2.0s and amplitude of swing 5.0cm. Calculate the maximum magnitude of the

(i) Velocity

(ii) Acceleration of the bob

SOLUTION

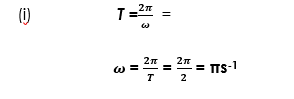
Therefore Velocity, (V) is a maximum at the equilibrium position where x = 0 and

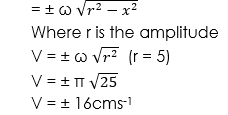
Maximum velocity, v of the bob = ± 16cms^-1

(ii) Acceleration a is maximum at the limits of the swing where x = r = ± 5cm and a = ω²r

Therefore maximum acceleration, a_max = π² x 5 cms-1

a_max = π² x 5 = 50cms-1

Free Oscillations

When a body which can oscillate about its mean position is displaced from the mean position and then released, it oscillates about its mean position. These oscillations are called free oscillations and the frequency of oscillations is called natural frequency.

Damped Oscillations

Oscillations with a decreasing amplitude with time are called damped oscillations.

Un-damped Oscillations

Oscillations with a constant amplitude with time are called un-damped oscillations.

Forced Oscillations

Oscillations of any object with a frequency different from its natural frequency under a periodic external force are called forced oscillations.

Resonant Oscillations

When an external force is applied on a body whose frequency is an integer multiple of the natural frequency of the body, then its amplitude of oscillation increases and these oscillations are called resonant oscillations.

 

We hope you enjoyed the class.

Should you have any further question, feel free to ask in the comment section below and trust us to respond as soon as possible.

Ready to make school management and growth easy? Book your free onboarding session now

Get more class notes, videos, homework help, exam practice on Android [DOWNLOAD]

Get more class notes, videos, homework help, exam practice on iPhone [DOWNLOAD]