Back to: PHYSICS SS2
Welcome to class!
In today’s class, we will be talking about the refraction of light. Enjoy the class!
Refraction of Light
Refraction is the bending (change in direction) of a ray of light when it crosses from one medium to another (e.g. air to glass).
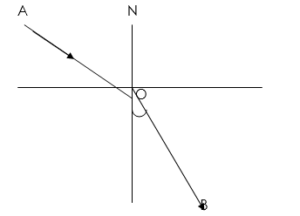
AO = incident ray
NO = Normal
OB = refracted ray
i = angle of incidence
r = angle of refraction
The Speed of light is different in different media. For instance, light travels faster in air than in glass. Thus when light crosses from one medium to another, there is a change in its velocity. Refraction then takes place.
Laws of Refraction
The laws of refraction are:
- The incident ray, the refracted ray and the normal at the point of incidence all lie on the same plane.
- For a given pair of media, the radius of the sine of the angle of incidence to the sine of the angle of refraction is a constant. It is also known as Snell’s law.
That is sin i/sin r (that is called Snell’s law)
n = sin i/sin r
n = refractive index
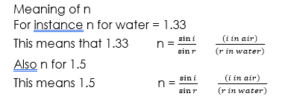
The higher the refractive index of a medium, the optically denser the medium is. For air, refractive index n = 1. This means that water with refractive index 1.33 is optically denser than air.
Real and Apparent Depth
When one looks into the deep pool water. It appears shallower. One sees a false depth. Likewise, if you place a glass block on the writings on the page the letters’ come closer to you’. The false depth is called the apparent depth while the actual depth is called real depth.
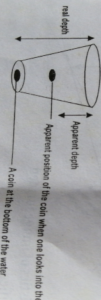
Refractive index = real depth/apparent depth
Refraction in Lenses
There are two main types of lenses concave (diverging) and convex (converging) lenses. All other types of lens are variants of the two below.
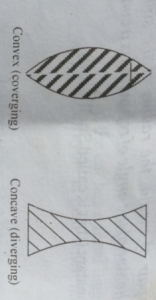
When parallel rays fall on a convex lens, they are refracted to converge at a point, its focus, hence the name converging lens. The concave lens on the other hand after refraction diverge lens.
Note:
A convex lens is converging while the concave mirror is converging. Also, concave lens diverging while convex mirror diverging.
Formation of images in Lens
-
Object between 2f and f
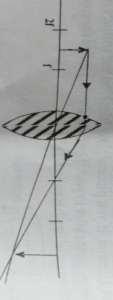
Characteristics of the image formed
(i) Magnified
(ii) Inverted
(iii) Real
(iv) Formed beyond 2f at the opposite side of the lens
-
Object between F and the lens
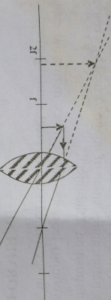
Characteristics of the image formed
(i) Image is virtual
(ii) Image is formed on the same side with the object
(iii) Image is erect
(iv) Image is magnified
-
Object at 2f
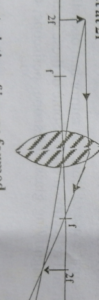
Characteristics of the image formed
(i) Image is the same as the object
(ii) Image is real
(iii) Image is inverted
(iv) Image is formed at 2f at the opposite side
-
Object beyond 2f
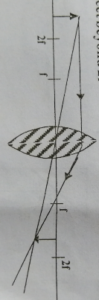
Characteristics of the image formed
(i) Image is formed between f and 2f at the opposite side
(ii) Image is diminished
(iii) Image is inverted
(iv) Image is real
A lens forms image by the refraction of light as shown above. Image formation in a convex lens is very similar to image formation in a concave mirror. Hence the nature and position of the image formed by a converging lens depend on the position of the object.
For concave (diverging) lens, just like a convex mirror, no matter the position of the object, an image formed is usually erect, diminished and virtual.
LENS FORMULAE
The object distance (u), and image distance (v) are related to the focal length of the lens by the lens formula
Applications of Convex Mirrors
- It is used as Car driving mirrors.
- It is used as a security mirror in super market
- Use as shaving mirror
- Use as a mirror
Refraction through Prism
There are two types of prisms namely:
- Rectangular Prism
- Triangular prism
Rays are produced from rectangular prism which has the angle of refraction either produced from the normal or produced to the normal, but rays transmitted through a triangular prism are always refracted towards the normal and close to the base of the triangular prism.
- The angle of incidence, i
- The angle of refraction, r
- The angle of emergence, e
- Minimum deviation, dm
- Equilateral angle, A
A = 60°, if the prism is equilateral. NB:
Minimum deviation, Dm of the light occurs when the ray passes symmetrically through the prism.
Refractive index of an equilateral triangular prism
Critical angle
The critical angle is the angle of incidence in the denser medium when the angle of refraction in the less dense medium is 90°. It is denoted by C.
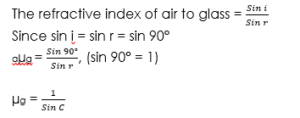
Total internal refraction
When the angle of incidence exceeds the critical angle, there exists no reflection and a total reflection occurs. This phenomenon is called total internal reflection.
The conditions under which total internal reflection occurs are:
- Light rays must travel through a denser medium to a less dense medium
- The angle of incidence must exceed a critical angle.
Applications of Total Internal Reflection
The principle of total internal reflection is adopted in the invention and operation of the following:
- Binoculars
- Mirage
- Optical fibres
- Total internal reflection of radio waves is employed
- Refractometer
- Total reflecting prisms are employed in periscopes, prism binoculars, projection lanterns and cameras.
WORKED EXAMPLES
(1) If the angle of incidence i on an air water boundary is 60°, calculate the angle of refraction r (ŋ = 4/3
SOLUTION
sin i/sin r = sin 60/sin r
n = 4/3
sin r = 4/3 sin 60 = 0.6495
In our next class, we will be talking about Optical Instruments. We hope you enjoyed the class.
Should you have any further question, feel free to ask in the comment section below and trust us to respond as soon as possible.
Get more class notes, videos, homework help, exam practice on Android [DOWNLOAD]Get more class notes, videos, homework help, exam practice on iPhone [DOWNLOAD]