Angles and Polygons

Back to: MATHEMATICS JSS 2

Welcome to JSS2 Third Term!

We are eager to have you join us in class!!

In today’s Mathematics class, We will be discussing Angles and Polygons. We hope you enjoy the class!

CONTENT: (i) Sum of interior angles of a polygon

(ii) Sum of exterior angles of a polygon

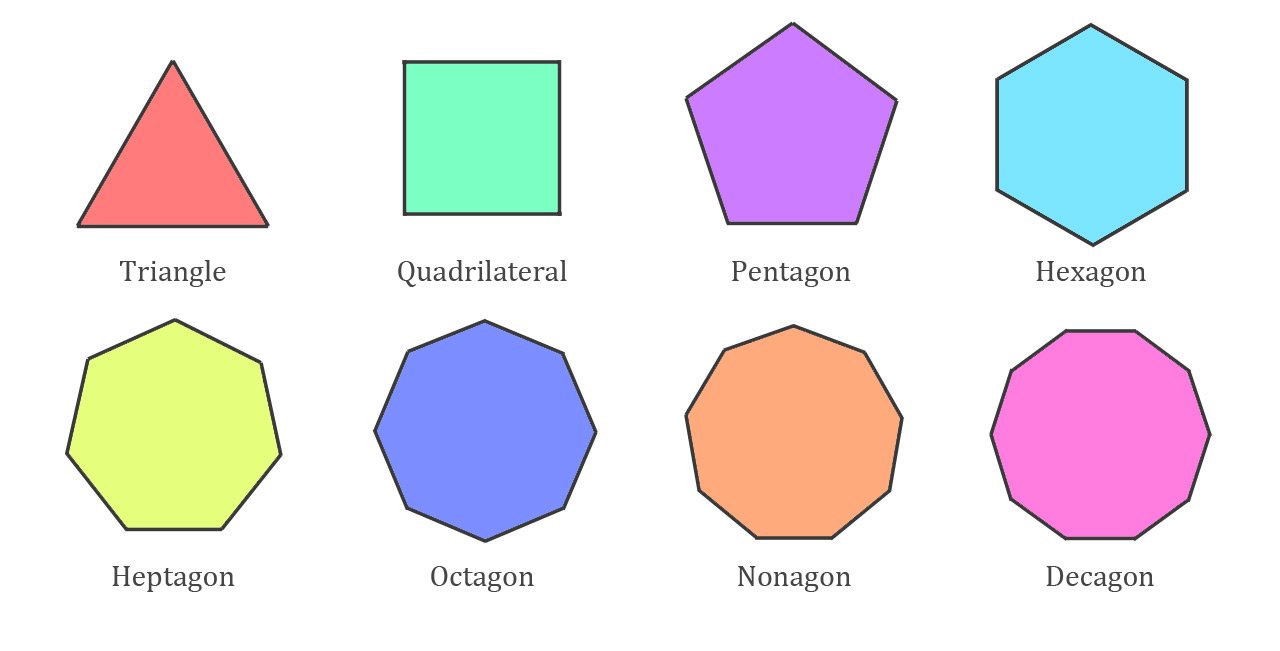
DEFINITION OF A POLYGON

A polygon is any close plane figure with a straight side. A regular polygon has all sides and angles equal.

Polygons are named according to the number of sides they have. Examples are:

Triangle a 3- sided polygon

Quadrilateral a 4- sided polygon

Pentagon a 5- sided polygon

Hexagon a 6- sided polygon

Heptagon a 7- sided polygon

Octagon an 8- sided polygon

Nonagon a 9- sided polygon

Decagon a 10- sided polygon

The diagrams below represent some common polygons.

Reference

NGM Book 2

Essential Mathematics for junior secondary school Book 2, chapter 9, pages 87 – 88

Sum of Interior Angles of a Polygon

The angles inside a polygon are called its interior angles as shown in the figure below:

The number of triangles depends on the number of sides of the polygon. For a polygon with ‘n’ sides, there will be (n-2) triangles. The sum of angles of a triangle is 180⁰.

Alternatively, since 180⁰ = (n-2) x 2 x 90

= 2(n-2) 90

= (2n-4) 90

Thus, the sum of the angles of an n-sided polygon can be represented as (n-2) 180⁰ or (2n-4) 90⁰

The table below shows the sum of interior angles of a regular polygon of a 3 sided polygon up to a sided polygon.

Polygon	No. of Sides	No. of Triangles (n-2)	Sum of interior Angles (n-2) 180⁰
Triangle	3	3 – 2 = 1	1 x 180⁰ = 180
Quadrilateral	4	4 – 2 = 2	2 x 180⁰ = 360⁰
Pentagon	5	5 – 2 = 3	3 x 180⁰ = 540⁰
Hexagon	6	6 – 2 = 4	4 x 180⁰ = 720⁰
Heptagon	7	7 – 2 = 5	5 x 180⁰ = 900⁰
Octagon	8	8 – 2 = 6	6 x 180⁰ = 1080⁰
Nonagon	9	9 – 2 = 7	7 x 180⁰ = 1260⁰
Decagon	10	10 – 2 = 8	8 x 180⁰ = 1440⁰

Worked Examples:

Calculate the size of an exterior angle of a regular nonagon (9 sides)
Calculate the size of an exterior angle of a regular hexagon (6 sides)

Answer to the evaluation questions

Sum of the exterior of a polygon = 360⁰. Number of sides of a nonagon = 9

$S i z e o f e a c h e x t e r i o r a n g l e = \frac{s u m o f e x t e r i o r a n g l e s / n u m b e r}{n u m b w e o f s i d e s} = \frac{360^{o}}{9} = 40^{o}$

Sum of exterior angles = 360^o

Hexagon has 6 sides.

= 60^o

GENERAL EVALUATION

The interior angles of a triangle add up to …………………………
The interior angles of a quadrilateral add up to ………………………
The sum of the interior angles of a regular polygon is 1080^o. How many sides has the polygon?

REVISION QUESTION

Calculate the number of sides of each of a regular polygon whose interior angle is 162^o
The sum of the 3 angles of a hexagon is 345^o. If the other angles are equal. Find the sizes of each of the angle.

READING ASSIGNMENT

Essential Mathematics for junior secondary school Book 2, Chapter 19, page 252 – 255

Exercise 19.5 No 1 page 255

WEEKEND ASSIGNMENT

The sum of the interior angles of a regular pentagon is A. 240^o B. 720^o C. 540^o D. 640^o
Calculate the size of each exterior angle of a regular hexagon. A. 60^o B. 30^o C. 45^o D. 125^o
The size of each angle of a regular octagon will be ____ A. 95^o B. 75^o C. 105^o D. 135^o
How many sides has a polygon if the sum of interior angles of that polygon gives 3240^o? A. 18^o B. 15^o C. 17^o D. 20^o
Calculate the size of each exterior angles of a pentagon A. 30^o B. 72^o C. 60^o D. 90^o

THEORY

Calculate
- - A. The total internal angels of an octagon
  - B. The size of each angle of a regular octagon
Calculate the
1. - Exterior angle
  - The number of sides of a regular polygon with an interior angle of 72^o