Linear  inequalities 

Back to: MATHEMATICS JSS 2

 

Welcome to Class !!

We are eager to have you join us !!

In today’s Mathematics class, We will be discussing Linear Inequalities. We hope you enjoy the class!

 

 

CONTENT

• Greater than and less than
• Properties of linear inequalities
• Not greater than and not less than
• Graphs of inequalities.

 

 

Greater than and less than

5 + 3 = 8 means equal to

X = 0 means x is not equal to 0

But 5 + 5 > 8, where 7 means greater than

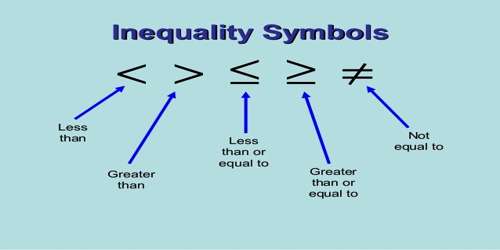
Similarly, 3 x 2 < 8 where < means less than, > and < are inequality symbols.

 

 

 

READING ASSIGNMENT

New General Mathematics UBE Edition, Chapter 22, pgs 209-211

Essential Mathematics by A. JS. Oluwasanmi Chapter 23 pgs 237-239

 

 

Properties of a linear inequality. The symbol > and < can be used to change word statements into algebraic statements. 

Worked Examples

1. The distance between two villages is over 18km. write this as an inequality statement.
2. I have x naira, I spend N20, the amount I have left is less than N5. Write inequality in x.
3. The area of a square is less than 25cm2. What can be said about
4. the length of its sides b. its perimeters

Solution

(1) x > 18

(2) I spent N20 out of x naira

Amount left = N(x – 20)

Less than N5  N(x – 20 ) < N5 i.e.  X – 20 < 5

 

(3) let the length be a , then a² < 25

a <   25,   a < 5

 

(4) perimeter = 4a since a = 4

then 4a < 4 x 5

4a < 20

a < 5cm

 

EVALUATION

1. Write the inequality symbols places of the statements below:
2. The car use more than 28 litres of petrol.
3. The cost of the stamp was less than N25.
4. The students got over 60% in the exam.
5. A boy saved over N500. His father gave him N200, the boy now had altogether. Write an inequality in y.
6. The perimeter of a square is less than 28cm what can be said about:
7. its length b. its area

 

READING ASSIGNMENT

New General Mathematics UBE Edition, Chapter 22, pgs 213-215

Essential Mathematics by A. JS. Oluwasanmi Chapter 23 pgs 237-239

 

 

NOT GREATER THAN AND NOT LESS THAN

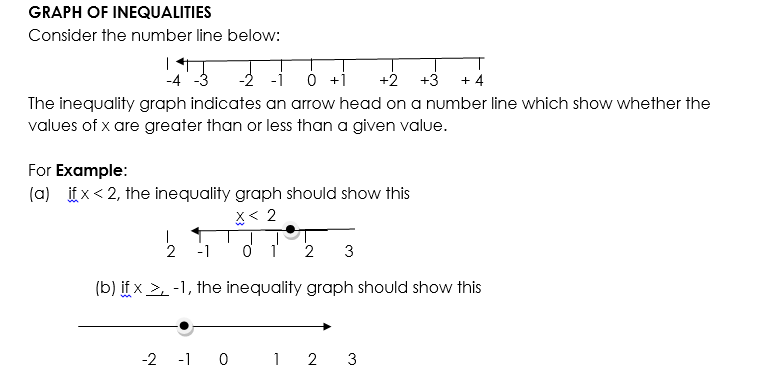
When a particular variable say x does not exceed a particular value, it means x is not greater than the given value.

For Example x <  50, it means x < 50 or x = 50; where  <  means less than or equal to. But when the variable x exceeds a given value for Example x > 50 or x = 50m it means less than or equal to. But when the variable x exceeds a given value for Example x > 50 or x = 50m it means x > 50 where >  means greater than or equal to .

 

Worked Examples

1. Notebooks cost N60 each Deborah has d naira it is not enough to buy a notebook. Taiwo has t naira. He is able to buy a notebook. What can be said about the value of d and it?

Solution

Deborah = d naira

Deborah amounts is less than N60 d < 60

Taiwo = t naira

In conclusion, t > d and d < t.

 

EVALUATION

1. Write an inequality in terms of the unknown.
   1. The number of goals n was five or more.
   2. the temperature tc was not greater than 38^oC.
   3. the number of students n was less than 36
   4. The pass mark in a test was 27, one person got x marks and failed. Another got y marks and passed, what can be said about x and y?

 

 

 

GENERAL EVALUATION

1. Say whether each of the following statement is true or false?
2. -20 is greater than – 5.
3. -3 x ( -2) > – 3 – 6
4. -18 <3 – 20
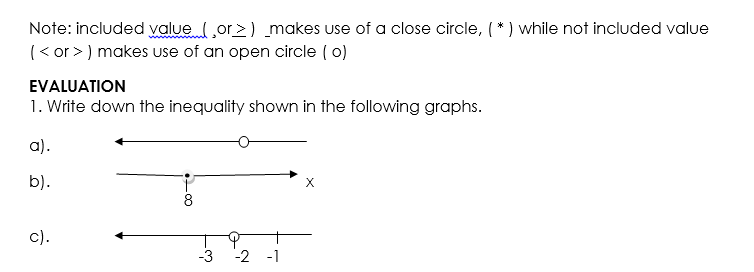
5. Illustrate the following on a number line
6. x > 0 b. x ≤ – 1                     c. x  ≥  -2

 

REVISION QUESTION

1. If x  is a positive integer, for what range of values of x  is 8 + 2x <  Draw number line to show your answer.
2. If x  is  an  integer, find  the  first  three  possible  values  of  x  in  the  inequality 6x – 5(x-2) ≤ 4 (2x-1)
3. If x is  a  positive integer  and  2x  +  3 >  -30 + 6p  (a) solve  for  x   (b) Find  all the  possible  values  of  x  and  show   them  on  a  number  line.

 

New General Mathematics UBE Edition, Chapter 22, pgs 213-215

Essential Mathematics by A. JS. Oluwasanmi Chapter 23 pgs 237-239

 

WEEKEND ASSIGNMENT

1. The inequality symbol for -1 is greater than -5 is  (A) – 1 < 5 (B) -5 > -1    (C) -1 > -5
2. The time for a journey t mins was over 2hrs the inequality statement is ……………… (A) t > 2hts B. 2hts > t   C. t  >  2hrs
3. The graph below represents thus

-2    -1     0    1    2 ½         3    4    5

(A) n > 2 ½  B. x < 2 ½   C  x < -2 ½

 

4. ( -3)² $\left[\right]$ 2²

The inequality symbol in the box is  (A) <  (B.) >   C. ≥

5. The cost of a stamp #x was not more than N20 (A) x > N20    (B.)  x = N20     (C.)  x  <  N20

 

THEORY

1. A square has an area of more than 36cm². What can be said about the length of one of its sides?
2. Sketch the following inequality on a graph.

(A) x ≤ – b                       b.   x ≥ 3.

 

 

Get more class notes, videos, homework help, exam practice on Android [DOWNLOAD]

Get more class notes, videos, homework help, exam practice on iPhone [DOWNLOAD]