Scale drawing of lengths and distances

Back to: MATHEMATICS JSS 2

 

Welcome to Class !!

We are eager to have you join us !!

In today’s Mathematics class, We will be discussing Scale Drawing of lengths and Distances. We hope you enjoy the class!

 

A drawing that shows a real object with accurate sizes except they have all been reduced or enlarged by a certain amount (called the scale).

The scale is shown as the length in the drawing, then a colon (“:”), then the matching length on the real thing.

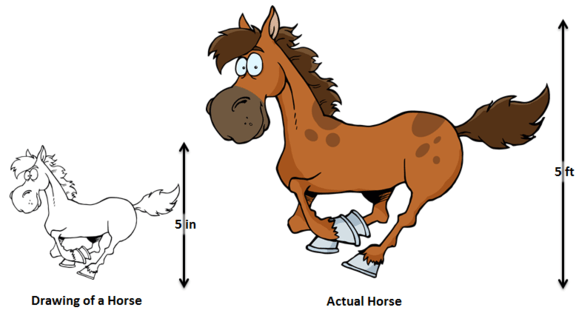
Example: this drawing has a scale of “1:10”, so anything drawn with the size of “1” would have a size of “10” in the real world, so a measurement of 150mm on the drawing would be 1500mm on the real horse.

Since it is not always possible to draw on paper the actual size of real-life objects such as the real size of a car, an aeroplane, we need scale drawings to represent the size like the one you see below of a van.

 

 

In real-life, the length of this van may measure 240 inches. However, the length of a copy or print paper that you could use to draw this van is a little bit less than 12 inches

Since 240/12 = 20, you will need about 20 sheets of copy paper to draw the length of the actual size of the van

In order to use just one sheet, you could then use 1 inch on your drawing to represent 20 inches on the real-life object

You can write this situation as 1:20 or 1/20 or 1 to 20
Notice that the first number always refers to the length of the drawing on paper and the second number refers to the length of a real-life object.

 

Example

Suppose a problem tells you that the length of a vehicle is drawn to scale. The scale of the drawing is 1:20 If the length of the drawing of the vehicle on paper is 12 inches, how long is the vehicle in real life?
Set up a proportion that will look like this:

$\frac{Length of drawing}{Real length} = \frac{1}{20}$

Do a cross product by multiplying the numerator of one fraction by the denominator of the other fraction
We get :
Length of drawing × 20 = Real length × 1
Since the length of drawing = 12, we get:
12 × 20 = Real length × 1
240 inches = Real length

 

Example
The scale drawing of this tree is 1:500
If the height of the tree on paper is 20 inches, what is the height of the tree in real life?

 

 

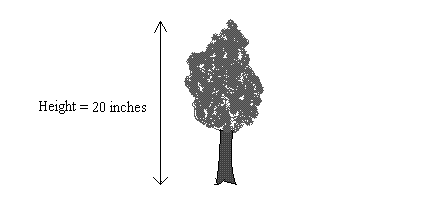
Set up a proportion like this:

$\frac{Height of drawing}{Real height} = \frac{1}{500}$

 

Do a cross product by multiplying the numerator of one fraction by the denominator of the other fraction
We get :
Height of drawing × 500 = Real height × 1
Since the height of drawing = 20, we get:
20 × 500 = Real length × 1
10000 inches = Real height

 

Scale Drawings

A map cannot be of the same size as the area it represents.  So, the measurements are scaled down to make the map of a size that can be conveniently used by users such as motorists, cyclists and bushwalkers.  A scale drawing of a building (or bridge) has the same shape as the real building (or bridge) that it represents but a different size.  Builders use scaled drawings to make buildings and bridges.

A ratio is used in scale drawings of maps and buildings.  That is:

The scale of a drawing = Drawing length: Actual length

Likewise, we have:

Map scale=Map distance: Actual distance
A scale is usually expressed in one of two ways:

Using units as in 1 cm to 1 km

Without explicitly mentioning units as in 1: 100 000.

 

Note

A scale of 1: 100 000 means that the real distance is 100 000 times the length of 1 unit on the map or drawing.

 

Example

Write the scale 1 cm to 1 m in ratio form.

Solution

1 cm to 1m = 1 cm : 1m

= 1 cm : 100 cm

= 1 : 100

 

Example

Simplify the scale 5 mm : 1 m.

Solution

5 mm : 1 m = 5 mm : 100 cm

= 5 mm : 1000 mm

= 5 : 1000

= 1 : 200

 

Example

Simplify the scale 5 cm : 2 km.

Solution

5 cm : 2 km = 5 cm : 2000 m

= 5 cm : 200 000 cm

= 5 : 200 000

= 1 : 40 000

 

Calculating the Actual Distance using the Scale

If the scale is 1: x, then multiply the map distance by x to calculate the actual distance.

Example

A particular map shows a scale of 1: 5000.  What is the actual distance if the map distance is 8 cm?

Solution

Scale = 1 : 5000 = 1 cm : 5000 cm

∴ Map distance : Actual distance = 1 : 5000

Map distance = 8 cm

Let the actual distance be a cm.

∴ 8 : a = 1: 5000 {Units are in cm}

$\frac{8}{a} = \frac{1}{5000}$ {Invert the fractions}

$\frac{a}{8} = \frac{5000}{1}$ {Multiply by 8}

$8 \times \frac{a}{8} = 8 \times 5000$

a = 40 000

∴Actual distance = 40 000 cm

= 40 000/100 m

= 400 m

 

Alternative Way

Map distance = 8 cm

Scale = 1 : 5000 = 1 cm : 5000 cm

∴ Map distance : Actual distance = 1: 5000

= 1 X 8 : 5000 X 8

= 8 : 40 000

∴ Actual distance = 40 000 cm

=40 000/100 m

=400m

 

Calculating the Scaled Distance using the Actual Distance

If the scale is 1: x, then divide the actual distance by x to calculate the map distance.

 

WEEKEND ASSESSMENT

A particular map shows a scale of 1 cm : 5 km.  What would the map distance (in cm) be if the actual distance is 14 km?

 

 

We have come to the end of this class. We do hope you enjoyed the class?

Should you have any further question, feel free to ask in the comment section below and trust us to respond as soon as possible.

In our next class, we will be talking about Solving Equations. We are very much eager to meet you there.

 

Get more class notes, videos, homework help, exam practice on Android [DOWNLOAD]

Get more class notes, videos, homework help, exam practice on iPhone [DOWNLOAD]