Fractions as Ratios, Decimals and Percentages

Back to: MATHEMATICS JSS 2

 

Welcome to Class !!

We are eager to have you join us !!

In today’s Mathematics class, We will be discussing Fractions as Ratios, Decimals and Percentages. We hope you enjoy the class!

 

Content

• Fractions and Percentages
• Proportion
• Ratio
• Rate

 

Fractions and percentages

A fraction can be converted to a decimal by dividing the numerator by its denominator. It can be changed to a percentage by simply multiplying by 100.

Example 5.1

• Change 3/8 into a decimal and percentage
• Convert 0.145 to a percentage

Solution

1)        3/8 = 0.375 in decimal

3/8 x 100% = 37.5%

 

2)        0.145×100=14.5%

 

 

To change a percentage to decimal fraction, simply divide by 100 and then convert to a decimal fraction. E.g. convert 92% to a decimal fraction.

Solution

$\frac{92}{100} = 0.92$

 

 

Example 5.3

1. Change the following to percentages

(a) 0.125 (b) 0.002

Solution

(a) 0.125×100% = 12.5%

(b) 0.002 = 0.002×100% = 0.2%

 

2. Change the following to decimal fractions

(A) 45 %   (b) 8/3%

Solution

$$\begin{gathered} 1. 45÷100 = \frac{45}{100} = 0.45 \\ 2. \frac{8}{3} ÷\frac{100}{1} = \frac{8}{3}\times \frac{1}{100} = \frac{8}{300} = \frac{4}{150} = \frac{2}{75} = 0.02666 \end{gathered}$$

 

 

Classwork

1. Change the following to percentage

(a) 0.264 (b) 0.875

2. Change the following to decimal fractions

(A) 60% (b) 52/3%

 

 

APPLICATION OF DECIMAL FRACTIONS AND PERCENTAGES

Consider the following examples.

1. 1. Find 15% of 2.8kg
   2. Express 3.3 mass a percentage of 7.5
   3. Find 331/3 % of 8.16litres

 

Solution

1. 15/100 of 2.8kg

15/100 x 2.8 x 1000g

15/100 x 2800

=420g

=420/1000

=0.420kg

 

2. 3.3/7.5 x 100/1

= 33/75 x 100/1

= 11×4 = 44%

 

3. 100/3% of 8.16litres

$$\begin{gathered} = \frac{100}{3}\% of 8.16 litres \\ = \frac{100}{3} \% \times 8.16 litres \\ = \frac{100}{3}\% \times 8.16 \times 1000 (1 litre = 1000 c{m}^3) \\ = \frac{100}{3}\% \times 8160 \\ convert the percentage to a fraction \\ = \left(\frac{100}{3} ÷ \frac{100}{1}\right) \times 8160 \\ = \left(\frac{100}{3} \times \frac{1}{100}\right) \times 8160 \\ =\left(\frac{1}{3}\right) \times 8160 = \frac{8160}{3} \\ = 2.720 litres \end{gathered}$$

 

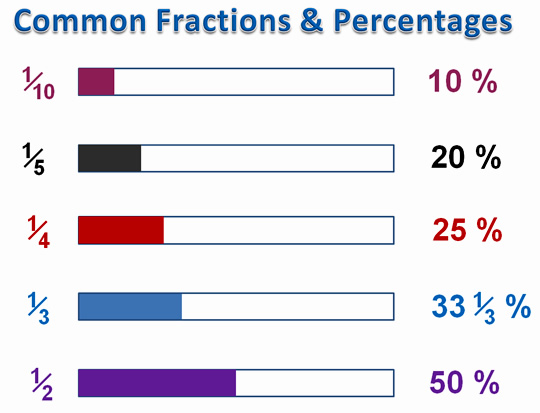
Classwork

1. Express1.5 as a percentage of 2.5 m
2. Find 662/3 % of2.4m

 

READING ASSIGNMENT

New General Mathematics, UBE Edition, chapter 1 Pages 78-79

Essential Mathematics by A J S Oluwasanmi, Chapter 1 pages 61-64

 

 

Proportion

Proportion can be solved either by the unitary method or inverse method. When solving by unitary method, always

• Write in a sentence, the quantity to be found at the end.
• decide whether the problem is either an example of the direct or inverse method
• Find the rate for one unit before answering the problem.

 

Examples

1. A worker gets N 900 for 10 days of work, find the amount for (a) 3 days (b) 24 days (c) x days

Solution

For 1 day  = N 900

1 day = 900/10 = N90

For 3 days =3 x 90 = 270

For 24 days = 24×90 = N 2,160

For x days =X x 90 = N 90 x

 

 

Inverse Proportion

Example 1: Seven workers dig a piece of ground in 10 days. How long will five workers take?

Solution

For 7 workers =10 days

For 1 worker =7×10=70 days

For 5 workers=70/5 =14 days

 

Example 2: 5 people took 8 days to plant 1,200 trees, How long will it take 10 people to plant the same number of trees 

Solution

For 5 people =8 days

For 1 person =8×5=40 days

For 10 people =40/10 =4 days

 

Class Work

1. A woman is paid N 750 for 5 days, Find her pay for (a) 1 day (b) 22 days
2. A piece of land has enough grass to feed 15 cows for x days. How long will it last (a) 1 cow (b) y cows
3. A bag of rice feeds 15 students for 7 days. How long would the same bag feed 10 students

Note on direct proportion: this is an example of direct proportion. The less time worked (3 days) the less money paid (#270) the more time worked (24 days) the more money paid (N N 2,160)

 

 

 

Ratio

Ratio behaves the same way as a fraction. Ratios are often used when sharing quantities.

Example

600/800=600/800=3/4

300:400 = 600:800 = 1200:1600 = 3:4

 

Example

1. Express the ratio of 96c: 120c as simple as possible

Solution 96c: 120c=96/120=4/5=4.5

 

2. Fill in the gap in the ratio of 2:7=28 

Solution

let the gap be X

2/7 = X/28

7X =2 x 28

X=2 x 28/7

X=2 x 4

X = 8

 

• Two students shared 36 mangoes in the ratio 2:3 How many mangoes does each student get?

Solution

Total ratio =2+3=5

First share=2/5×35/1=21 mangoes

 

 

Rate

Rate is the change in one quantity to the other. Examples are 45km/hr, a km, 1 litre etc

Worked examples

• A car goes 160 km in 2 hrs what is the rate in km/hr?

Solution

In 2 hrs the car travels 160 km

In 1 hr the car travels 160/2=80km

Therefore the rate of the car is 80km/hr

 

• A car uses 10 litres of petrol to travel 74 km. Express its petrol consumption as a rate in km per litre.

Solution

10 litres =74 km

1 litres = 74/10 km

=7.4 km

 

Classwork

1. A car factory made 375 cars in 5 days, Find its rate in cars per day.
2. A car travels 126 km in 11/2 hrs. Find the rate in km per hr.

 

READING ASSIGNMENT

New General Mathematics, UBE Edition, Chapter 1, pages 80-85

Essential Mathematics by A J S Oluwasanmi, Chapter 1, pages 69-72

 

WEEKEND ASSIGNMENT

1. 5 men build in 10 days, how long would it take 25 men?

(a) 3 days (b) 2 days (c) 5 days (d) 10 days

2. A girl buys 7 pens for N How would ten pens cost? (a)#300 (b)#30 (c)#3 (d)#200
3. Fill in the gap in m: a =16:24 (a) 10 (b) 12 (c) 4 (d) 6
4. Express 90km /hr: 120km /hr as simple as possible (a) 4:3 (b) 3:4 (c) 2:3 (d) 3:2
5. A factory makes N 2000 pencils in 10 days, Find its production rate of pencils per day (a) N 20 per day (b) N 100 per day(c) N 50 per day (d) N 200 per day

                                

THEORY

1. Find 50% of 3.5m

2. A bag of corn can feed 100 chicks for 12 days. How long would the same bag feed 80 chickens?

 

 

 

We have come to the end of this class. We do hope you enjoyed the class?

Should you have any further question, feel free to ask in the comment section below and trust us to respond as soon as possible.

In our next class, we will be talking about Household Arithmetric relating to Profit, Interest, Discount and commission. We are very much eager to meet you there.

 

Get more class notes, videos, homework help, exam practice on Android [DOWNLOAD]

Get more class notes, videos, homework help, exam practice on iPhone [DOWNLOAD]