Whole Numbers and Decimal Numbers, Multiples and Factors

Back to: MATHEMATICS JSS 2

 

Welcome to Class !!

We are eager to have you join us !!

In today’s Mathematics class, We will be discussing Whole Numbers Decimal Numbers. We will also be looking at Multiples and Factors of Numbers. We hope you enjoy the class!

 

Content

• Whole Difference between Whole Numbers and Decimal Numbers
• Whole numbers in Standard Form and Decimal Numbers in Standard Form
• Factors, Multiples and Prime Numbers

 

Difference between Whole Numbers and Decimal Numbers

A whole number is a number without fraction. For example 1, 2, 3, 4…1000, 38888 are examples of whole numbers. 71/2 is not a whole number. A decimal number is a fractional number less than 1. It is smaller to a whole number. Examples – 0.1, 0.01, 0.001etc

 

Whole Numbers in Standard Form and Decimal Numbers in Standard Form

Whole numbers in standard form are expressed in the form of A x 10ⁿ such that A is a number between 1 and 10, n is a whole number.

Example

Express the following in standard form (a) 200 (b) 4100 (c) 300000

Solution

• 200 = 2 x 100 = 2×10²
• 4100 = 4.1 x 1000 = 4.1 x 10³
• 300000 = 3 x 100000 = 3 x 10⁵

 

Evaluation

Express the following in standard form (a) 500 (b) 36000 (c) 7200000

 

 

Decimal fractions such as 0.00 and 0.000001 can be expressed as powers of 10

e.g. 0.0001 = 1/10000 = 1/10⁴ = 10^-4

Thus, any decimal fraction can be expressed in a standard form

e.g.  0.008= 8/1000= 8/10³ = 8×1/10³ = 8×10^-3

Therefore, the number 8×10^-3 is in standard form ax10 and n is a negative integer while A is a number between1 and 10

Example

Express the following in standard form (a) 0.0023 (b) 0.00034 (c) 0.125

Solution

• 023 = 23/1000 = 2.3/10² = 2.3 x 10^-3
• 00034 34/100000= 3.4/10⁴ = 3.4x 10^-4
• 125 = 125/1000 = 1.25/10¹ = 1.25×10^-1

 

Evaluation

Express the following in standard form (a) 0.0067 (b) 0.00082 (c) 0.012

 

READING ASSIGNMENT

New General Mathematics, UBE Edition, chapter 1, pages 27-28

Essential Mathematics by A J S Oluwasanmi, Chapter 1, pages 1-4

 

 

FACTORS, MULTIPLES AND PRIME NUMBERS

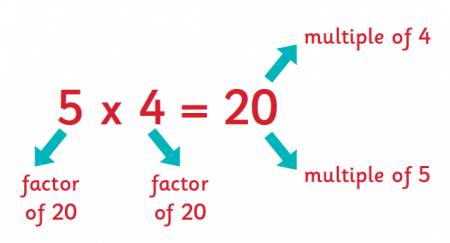
The factors of a number are the whole numbers that divide the number exactly. For example, the factors of 10 are 1, 2 and 5.

A prime number has only two factors, itself and 1. The following are examples of prime numbers 2, 3, 5, 7, 11, 13…. However, 1 is not a prime number.

 

A multiple of a whole number is obtained by multiplying it by any whole number.

 

Example

1. Write down all the factors of 18.
2. State which of these factors are prime numbers
3. Write the first three multiples of 18
4. Express 18 as a product of its prime factors in index form

 

Solution:

1. Factors of 18 are 1, 2,3,6,9 and 18.
2. Prime numbers of the factors of 18 are 2 and3
3. The first three multiples of 18 are 1×18 = 18, 2×18=36, 3×18=54 => 18, 36 and 54.
4. 18 = 2x3x3 = 2 x 3² in index form

 

Example 2:

1. Write down all the factors of 22.
2. State which of these factors are prime numbers
3. Write the first three multiples of 22

 

Solution:

1. Factors of 22 are 1, 2, and 11.
2. Prime numbers of the factors of 22 are 2 and11
3. The first three multiples of 22 are 1×22 = 22, 2×22=44, 3 x 22=66 => 22, 44 and 66.

 

Evaluation

1. Write down all the factors
2. State which of these factors are prime numbers
3. Write the first three multiples of each of the following numbers below
4. Express each as a product of its prime factors in index form

• • • (A) 12 (B) 30 (C) 39  (D)  48

 

READING ASSIGNMENT

New General Mathematics, UBE Edition, Chapter, 1 page 13-14

Essential Mathematics by A J S Oluwasanmi, Chapter 1, pages 1-4

 

WEEKEND ASSIGNMENT

1. Which of these is not a prime number (a) 2 (b) 5 (c) 7 ( d) 1
2. Express 360000 in standard form (a) 3.6 x 10⁵ (b) 3.6 x 10⁶ (c) 3.6 x 10³           (d)   3.6 x 10⁴
3. Express 0.000045 in standard form (a) 4.5 x 10^-2 (b) 4.5 x 10³ (c) 4.5 x 10^-5 (d) 4.5 x 10^-6
4. Which of these is not a factor of 42 (a) 9 (b) 6 (c) 7 (d) 2
5. Express 50 is product of its prime factor (a) 2 x 5² (b) 2 x 5 (c) 2² x 5² (d) 2 x 5

 

THEORY

1. For each number 42,45,48,50
2. Write down all its factors.
3. State which factors are prime numbers?
4. Express the number as a product of its prime factors.
5. Express the following in standard form (a) 345000 (b) 0.00034 (c) 0.125

 

 

 

We have come to the end of this class. We do hope you enjoyed the class?

Should you have any further question, feel free to ask in the comment section below and trust us to respond as soon as possible.

In our next class, we will be talking about LCM, HCF and Perfect Squares. We are very much eager to meet you there.

 

School Owner? Looking for ready-made content and tools to save time and grow easily? Book a free demo session now

Get more class notes, videos, homework help, exam practice on Android [DOWNLOAD]

Get more class notes, videos, homework help, exam practice on iPhone [DOWNLOAD]