Area Of Plane Figures

Back to: MATHEMATICS JSS3

 

Welcome to Class !!

We are eager to have you join us !!

In today’s Mathematics class, We will be talking about Area of Plane Figures. We hope you enjoy the class!

 

 

Area of Plane Figures

 

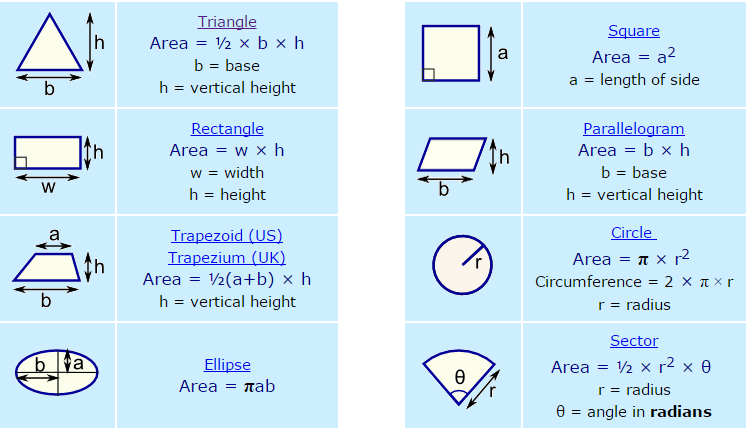
Area of Triangle

 

$$\begin{gathered} Sin A = \frac{h}{c} \\ h = c \times Sin A \\ Area of ∆ABC = \raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right. bc Sin A \end{gathered}$$

 

Example 1:

Find the area of triangle PQR if sides PQ = 6cm, PR = 8cm and QR  = 10cm

Solution

First, we need to show that ∆PQR is a right angled triangle

PQ²  +  PR2    =  QR2

6²  + 8²   =  10²

36  + 64  = 100

 

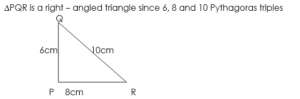
Area of ∆PQR   = $\frac{1}{2} \times 8 \times 6$= 24cm²

 

 

Example 2:

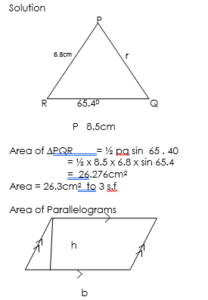
Calculate the area of triangle PQR correct to 3 significant figures if p = 8.5cm, q = 6.8cm and R = 65.4⁰

 

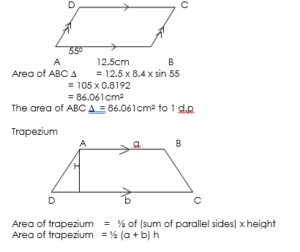
Parallelogram

Area of parallelogram  = base  x  height  =  bh

Consider the parallelogram

 

In general,

Area of parallelogram = product of adjacent sides x the size of the angle between the two sides

 

Example 3

Find the area of a parallelogram with base 12cm and height 7cm

Solution

Area of parallelogram = base x height

=  12cm  x 7cm

=  84cm²

 

Example 4:

Find the area of parallelogram shown in the diagram below

 

 

Rhombus

Area of Rhombus   = base x height =  bh

OR Area of Rhombus    =  $\frac{1}{2}$  of the product of diagonals

 

 

Trapezium

Area of Trapezium = $\frac{1}{2}(Base + Top) Height = \frac{1}{2}\left(AB + DC\right)h$

Example 3:

Find the area of trapezium  ABCD shown below if AB  = 8cm, BC = 6cm,  DC  = 12cm  and angle BCD  = 43⁰

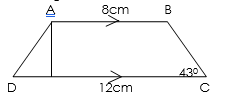
Solution:

Area of trapezium ABCD   = $\frac{1}{2} \times \left(AB + DC\right)h$

Sin 43⁰      = h/6

h   =   6 x sin 430

=  6 x 0.6821  =  4.092

 

Area of ABCD  =  ½  (8 + 12) x   4.092

= ½ x 20 x 4.0920    = 40.92cm²

 

 

 

 

 

READING ASSIGNMENT

Essential Mathematics page 220

Ex 21.5 ; 1 – 23

 

WEEKEND ASSIGNMENT

1. The area of a parallelogram is given as 108cm². F he height of the parallelogram is 9cm, find the base of the parallelogram  A. 13cm B. 9cm    C.  12cm
2. Find the area of a rhombus of side 20mm and height 10kk   A. 20mm²   B. 200mm²   C.  300mm²
3. Find the area of a circle of diameter 35cm
4. The area of a circle is 1386cm². Find the diameter of the circle A. 21cm  B. 42cm  C. 82cm
5. A sector of a circle of radius 8cm has an area of 120⁰ at the centre. Find its perimeter  A. 33  B.  34  C. 36

 

THEORY

1. A circle has an area of 144. Calculate the circumference of the circle, leaving your answer in terms of
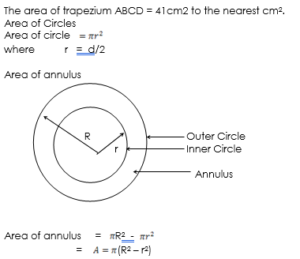
2. Calculate the area of an annulus, which has an external diameter of 25cm and internal diameter of 15cm.

 

 

We have come to the end of this class. We do hope you enjoyed the class?

Should you have any further question, feel free to ask in the comment section below and trust us to respond as soon as possible.

In our next class, we will be talking about Trigonometry. We are very much eager to meet you there.

 

Get more class notes, videos, homework help, exam practice on Android [DOWNLOAD]

Get more class notes, videos, homework help, exam practice on iPhone [DOWNLOAD]