Variation

Back to: MATHEMATICS JSS3

 

Welcome to Class !!

We are eager to have you join us !!

In today’s Mathematics class, We will be talking about Variation. We hope you enjoy the class!

 

 

Direct Variation

If a person buys some packets of sugar, the total cost is proportional to the number of packets bought.

The cost of 2 packets at Nx per packet is N2x.

The cost of 3 packets at Nx per packet is N3x.

The cost of n packets at Nx per packet is Nnx.

The ratio of the total cost to the number of packets is the same for any number of packets bought.

This is an example of direct variation or direct proportion. The cost, C, varies directly with the number of packets, n.

 

In another example, the mass, M, varies directly with the length, L.

 

The symbol ∝ means ’varies with’ or ‘is proportional to’. The statements in the previous paragraph are written:

C ∝ n

M ∝ L

M ∝ L really means that the ratio $\frac{M}{L}$  is constant (i.e. stays the same).

 

Example

1 packet of sugar costs x naira. What will be the cost of 20 packets of sugar?

Solution

Cost varies directly with the number of packets bought.

Cost of 1 packet  = x naira

Cost of 20 packets = 20 X x naira

= 20x naira

 

Example

C ∝ n and C = 5 when n = 20. Find the formula connecting C and n.

Solution

C ∝ n means $\frac{C}{n}$ = k.

0r C = kn

C = 5 when n = 20

hence  5 = k V 20

k = ¼

Thus, C = ¼n is the formula which connects C and n.

A formula such as C = ¼n is often known as a relationship between the variables C and n.

 

Exercise

1. 1m of wire has a mass of x g. What is the mass of 25 m of the same wire?
2. A man cycles 15 Km in 1 hour. How many will he cycle in t hours in he keeps up the same rate?
3. Eggs cost N25 each, how many will n eggs cost?

Answers

1. 25x g  2. 15t km  3. N25n

 

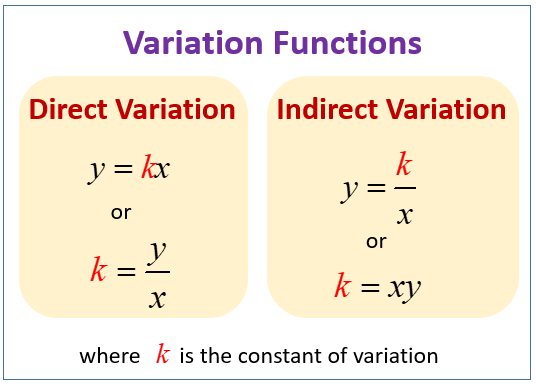
Inverse Variation

Inverse variation is the relationship of two variables such that one variable increases in its value as the other variable decreases and vice-versa i.e the two variables are inversely proportional to each other. In other words, it is defined as the mathematical expression that shows the relationship between two variables whose product is constant.

 

The Inverse Variation Formula is,

$Y = \frac{k}{x}$

Some solved problems on inverse variation are given below:

 

Examples

Question 1: If y varies inversely with x and when y = 100, x = 25. What is the value of y when x = 10?
Solution

Given,
y = 100
x = 25
The inverse variation formula is,
y = kx
100 = k25
k = 100 X 25
k = 2500
Now,
x = 10
k = 2500
y = kx
y = 250010
y = 250

 

Question

The time taken to reach the church is inversely proportional to the driving speed. If traveled at the speed of 30 miles per hour, it takes you 2 hours to reach the church. How long will it take to reach the church if moving at a speed of 60 miles per hour?
Solution:

Given,
y = 2
x = 30
The direct variation formula is,
y = kx
2 = k30
k = 2 X 30
k = 60

Now,
x = 60
k = 60
y = kx
y = 6060
y = 1

 

 

Joint variation

The mass of a sheet of metal is proportional to both the area and the thickness of the metal. Therefore M ∝ At (where M, A and t are the mass, area and thickness). This is an example of joint variation. The mass varies jointly with the area and thickness.

At midday, the temperature, T⁰C, inside a house is proportional to the outside temperature, S⁰C, and inversely proportional to the thickness of the house walls, t cm. In this case,

$T \propto \frac{s}{t}$ This is another example of joint variation.

The inside temperature varies directly with the outside temperature and inversely with the wall thickness.

 

Example

x ∝ $\frac{y}{z}$ . When y = 7 and z = 3, x = 42.

1. Find the relation between x, y and z.
2. Find x when y = 5 and z = 9.

Solution

1) x ∝ y/z

Thus, x = ky/z, where k is a constant.

When y = 7 and z = 3, x = 42.

Thus, 42 = k X 7/3

K = 3 X 42/7 = 18

Hence x = 18y/z

 

2) When y = 5 and z = 9,

x = 18 X 5/9 = 2 X 5

x = 10

 

Exercise

1. x ∝ yz. When y = 2 and z = 3, x = 30.
2. Find the relationship between x, y and z.
3. Find x when y = 4 and z = 6.
4. x ∝ y/z. x = 27 when y = 9 and z = 2.
5. Find the relationship between x, y and z.
6. Find x when y = 14 and z = 12.

 

 

Partial variation

When a tailor makes a dress, the total cost depends on two things: first the cost of the cloth; secondly the amount of time it takes to make the dress. The cost of the cloth is constant, but the time taken to make the dress can vary. A simple dress will take a short time to make; a dress with a difficult pattern will take a long time. This is an example of partial variation. The cost is partly constant and partly varies with the amount of time taken. In algebraic form, C = a + kt, where C is the cost, t is the time taken and a and k are the constants.

 

Example

R is partly constant and partly varies with E. When R = 530, E = 1 600 and when R = 730, E = 3 600.

1. Find the formula which connects R and E.
2. Find R when E = 1 300.

 

Solution

From the first sentence,

R = c + kE where c and k are both constants.

Substituting the given values gives two equations.

530 = c + 1 600k (1)

730 = c + 3 600k (2)

These are simultaneous equations.

Subtract (1) from (2).

200 =  2 000k

k = 200/2 000

=1/10

Substituting in (1),

530 = c + 1 600 X 1/10

530 = c + 160

Thus, c = 370

Thus, R = 370 + 1/10E is the required formula.

1. R = 370 + E/10

When E = 1 300,

R = 370 + 1 300/10

= 370 + 130

= 500

 

 

 

We have come to the end of this class. We do hope you enjoyed the class?

Should you have any further question, feel free to ask in the comment section below and trust us to respond as soon as possible.

In our next class, we will be talking about Statistics. We are very much eager to meet you there.

 

For more class notes, homework help, exam practice, download our App HERE

Join ClassNotes.ng Telegram Community for exclusive content and support HERE