Trigonometry

Back to: MATHEMATICS JSS3

 

Welcome to Class !!

We are eager to have you join us !!

In today’s Mathematics class, We will be talking about Trigonometry. We hope you enjoy the class!

 

TRIGNOMETRICAL RATIO

The trigonometrical ratio is a ratio of the lengths of two sides of a right-angle triangle. The three trigonometrical ratios are sine (sin) cosine (cos) and tangent (tan). The word tri- means three, thus trigonometrical ratio deals with three-sided figure (triangle).

 

In a right-angled triangle, the longest side is called the hypotenuse (opp the right angle), the side adjacent (next) to the given angle is called the Adjacent while the side opposite to the given angle is called the opposite.

 

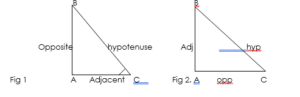
Note: To be able to know the ratio easily take note of the acronym SOHCAHTOA.

Where S stands for sine, C stands for cosine, T for Tangent, O for Opposite, H for Hypotenuse and A for Adjacent.

 

Degree and Minutes

Angles are often measured to the nearest degree. In some situations, degrees may be subdivided into minutes.

Note:

1⁰ =60 minutes. This is written as 60^/.

To change from minutes to degrees, we divide the number by 60.

 

Example: convert 10⁰ to minutes

Solution: 10 x 60 = 600mins

 

EVALUATION:

1. Convert the following to minutes: A. 16⁰   B. 50⁰
2. Rewrite and give your answer in degree to 1.dp A. 46⁰ 15¹  B. 39⁰ 25¹  C. 140⁰ 4

 

 

SINE OF ANGLE

In a right-angled triangle, the ratio of the opposite to hypotenuse is defined as the sine of the angle under consideration. this can be easily remembered using SOHCAHTOA.

SOH here means Sine = $\frac{Opposite}{Hypotenuse}$

 

From fig 1, sin ø = AB/BC. The ratio does not depend on the size of the triangle but depends only on the size of the angle (ø).

To find the sine of the angles, we use either a calculator or the sine table. In the use of sine table, since the sine of angle increases as the angle increases, thus the differences will be added.

 

EVALUATION

Use a mathematical table to find

• sin 43
• sin 14.58
• sin 30.6

 

 

USE OF SINE IN SOLVING TRIANGLES

Example:

Find the marked side of the angle in each of the following. Give your answer to 2.s.f.g.

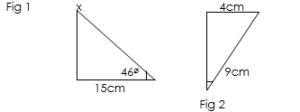
Solution:                                                    From Fig 2

From fig 1                                                sinø = opp/hyp

Sin46 = 15/x                                             sinø =4cm/9cm

X=15/sin46                                              sinø = 0.444

X = 15/0.7193                                          ø = sin¹ 0.4444

X=20.85,     X=21 (2.s.f.g)                      ø = 26.49, ø= 26 (2.s.f.g)

 

EVALUATION

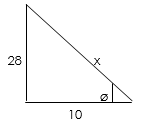
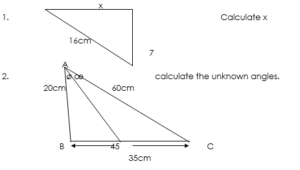
What is the value of X and ø in the below triangle

 

 

COSINE OF ANGLES

In a right-angled triangle, the ratio of adj/hyp is defined as the angle under consideration.

this can be easily remembered using SOHCAHTOA.

CAH here means Cosine = $\frac{Adjacent}{Hypotenuse}$

Using diagram:

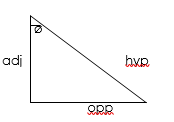
Thus Ө = AB/AC

This value of the ratio does not depend on the size of the triangle but on the size of the angle.

 

CALCULATIONS OF COSINE OF ANGLES

Find the unknown side or angle in the below triangles

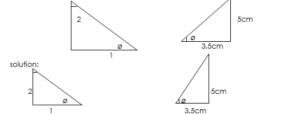
cosø = Adj/hyp                                              cosø = adj/hyp

cosø = ½                                                     cosø = 3.5cm/ 5cm

ø = cos¹ 0.5                                                     ø = cos¹ 0.7

ø = 60⁰                                                        ø = 45.67

 

 

 

TANGENT OF ANGLES

The tangent of any angle is the ratio opp/adjacent.

this can be easily remembered using SOHCAHTOA.

TOA here means Tangent = $\frac{Opposite}{Adjacent}$

In short form, tanӨ = opp/adj

 

CALCULATING TANGENT OF TRIANGLES

Examples: find the side of the triangle marked x. correct to 2 S.F.G in the figure below.

 

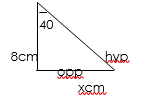
solution:

tan ø = opp/adj = xcm/8cm

tan ø = x/8,  ø = tan 40 x 8

ø = 0.8391×8

ø = 6.7128;  ø = 6.7( 2 s.f.g)

 

EVALUATION: calculate the side of the triangle marked x

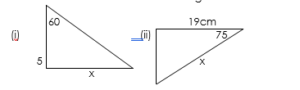
READING ASSIGNMENT

Essential mathematics for J.S.S 3 Pg 101-116

Exam Focus for J.S.C.E. for J.S.S 3    Pg 224-235

 

WEEKEND ASSIGNMENT

1. Convert 32.4⁰ to degree and minutes. A. 32 42 ¹ 32 44¹ C. 32 24¹
2. Cos 60 is equal to ——- A. 0.5 B. 0.49 C. 1/25
3. Calculate the side marked P, Q, and α

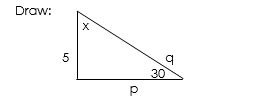
1. 1. 1. the value of P is 9.6 B. 8.7 C. 10
      2. the value of q is — A. 10 B. 8 C. 13
      3. the value of α is —A. 45 B.60 C. 30

 

Theory

 

 

 

We have come to the end of this class. We do hope you enjoyed the class?

Should you have any further question, feel free to ask in the comment section below and trust us to respond as soon as possible.

In our next class, we will be talking about “Angles of Elevation and Depression”. We are very much eager to meet you there.

 

Get more class notes, videos, homework help, exam practice on Android [DOWNLOAD]

Get more class notes, videos, homework help, exam practice on iPhone [DOWNLOAD]