SCALE DRAWING

Back to: MATHEMATICS JSS3

 

Welcome to Class !!

We are eager to have you join us !!

In today’s Mathematics class, We will be talking about Scale Drawing. We hope you enjoy the class!

 

 

Using Scales

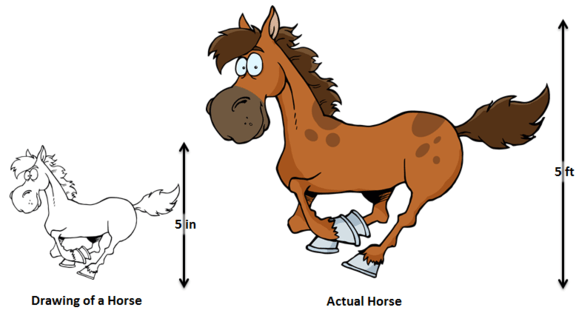
A scale is a ratio or proportion that shows the relationship between a length or a drawing and the corresponding length on the actual object.

Thus,

$\mathit{S}\mathit{c}\mathit{a}\mathit{l}\mathit{e}\mathbf{ }\mathbf{=}\mathbf{ }\frac{\mathbf{A}\mathbf{n}\mathbf{y}\mathbf{ }\mathbf{l}\mathbf{e}\mathbf{n}\mathbf{g}\mathbf{t}\mathbf{h}\mathbf{ }\mathbf{o}\mathbf{n}\mathbf{ }\mathbf{s}\mathbf{c}\mathbf{a}\mathbf{l}\mathbf{e}\mathbf{ }\mathbf{d}\mathbf{r}\mathbf{a}\mathbf{w}\mathbf{i}\mathbf{n}\mathbf{g}}{\mathbf{C}\mathbf{o}\mathbf{r}\mathbf{r}\mathbf{e}\mathbf{s}\mathbf{p}\mathbf{o}\mathbf{n}\mathbf{d}\mathbf{i}\mathbf{n}\mathbf{g}\mathbf{ }\mathbf{l}\mathbf{e}\mathbf{n}\mathbf{g}\mathbf{t}\mathbf{h}\mathbf{ }\mathbf{o}\mathbf{n}\mathbf{ }\mathbf{a}\mathbf{c}\mathbf{t}\mathbf{u}\mathbf{a}\mathbf{l}\mathbf{ }\mathbf{o}\mathbf{b}\mathbf{j}\mathbf{e}\mathbf{c}\mathbf{t}}$

 

Worked Examples

1. The scale drawing of the length of an advertisement billboard measures 5cm. What is the actual length of the billboard if the scale is 1cm represents 2m?

Solution

1cm represents 2m

5cm represents 5 × 2m = 10m

The actual length of the billboard = 10m.

 

2. An airport runway measuring 6000m is drawn to a scale of 1cm represents 500m. Find its length on the drawing.

          Solution

500m is represented by 1cm

1m is represented by 1/500cm

6000m is represented by 6000 × 1/500 = 12cm

Length on drawing = 12cm

 

Evaluation:

1) Copy and complete the table below in finding the length on drawing giving a suitable scale.

Actual length	Scale	Length on drawing
20m	1cm to 5m
450m	1cm to 100m
65m	1cm to 5m

 

2) Copy and complete the table by finding the actual length.

Length on drawing	Scale	Actual length
11cm	1cm to 5m
8.2cm	1cm to 100m
12.6cm	2cm to 1m

 

Scale Drawing

Scale drawing is very important to engineers, architects, surveyors and navigators. For an accurate scale drawing, mathematical instruments are needed such as pencils, a ruler and a set-square. Also, the dimensions of the actual objects are written on the drawing.

 

Worked Examples

1. A rectangular field measures 45m by 30m. Draw a plan of the field. Use measurement to find the distance between opposite corners of the field.

Solution

Firstly, make a rough sketch of the plan

45m

30m

 

 

 

Secondly, choose a suitable scale

Using 1cm represent5m will give a 9cm by 6cm rectangle.

The distance between the opposite corners of the field is represented by the dotted line. Length of the dotted line = 10.75

Actual distance = 10.75 × 5 = 53.75m = 54m (to the nearest metre)

 

 

Example 2:

Points A and B are 178m and 124m from X respectively. The distance between A and B is 108m. Make a scale drawing of the path and find the angle between the paths and X.                                                           X

Solution

178m               124m

 

 

A                            B

108m

Using a suitable scale of 1cm to 20m, the sides of the triangle in scale drawing will be as follows:

AX = 178/20 = 8.9cm, BX = 124/20 = 6.2cm, AB = 108/20 = 5.4cm.

X

 

 

 

 

 

178m                     124m

 

 

A         108m             B

Using a protractor, AXB = 37⁰ (to the nearest degree). The angle between the paths is 37⁰.

 

 

Evaluation:

• Find the distance between the opposite corners of a rectangular room which is 12m by 9m. Use a scale of 1cm to 3m.
• A triangular plot ABC is such that AB = 120m, BC = 80m and CA = 60m. P is the middle point of AB. Find the length of PC. Use a scale of 1cm to 10m.

 

 

Application of Scale Drawing on Related Problems

Worked Examples

• The scale on a map is 1: 50,000.

a) Two villages A and B on the map are 5.5cm apart, find the actual distance in km between A and B.

b) If town C is 4km from the village A, what is the distance of C from A on the map?

Solution

$$\begin{gathered} Note: Map Scale = \frac{Actual dis\tan ce}{dis\tan ce on the map} \\ \therefore Dis\tan ce on map = \frac{Actual dis\tan ce}{Map scale} \end{gathered}$$

 

a) 1cm represents 50,000cm

5.5cm represent 50,000 × 5.5 = 275,000cm

To correct to km = 275,000/100,000 = 2.75km.

 

b) 1km = 100,000cm

4km = 100,000 × 4 = 400,000cm.

Since 50,000cm represents 1cm

400,000cm is represented by 400,000/50,000 = 8cm

or Distance on the map = Actual distance / Map Scale

= 400,000 / 50,000 = 8cm.

 

 

Example 2:

Two cities are 70km apart. The distance between them is 20cm on the map. What is the scale of the map?

Solution

1km = 100,000cm

∴ 70km = 100,000 × 70 = 7,000,000cm

Map scale = actual distance/distance on map.

= 7,000,000/20 = 350,000

The scale of the map = 1: 350,000.

 

 

 

We have come to the end of this class. We do hope you enjoyed the class?

Should you have any further question, feel free to ask in the comment section below and trust us to respond as soon as possible.

We have come to the end of this term. It’s been a remarkable journey and we are glad that you have made it this far. For making it this far, we commend you for being resilient, you have taken charge of your education and future.

The Journey still continues though, we are moving on to Third term. we hope to meet you there. 

 

Get more class notes, videos, homework help, exam practice on Android [DOWNLOAD]

Get more class notes, videos, homework help, exam practice on iPhone [DOWNLOAD]