Whole Numbers

Back to: MATHEMATICS JSS3

Welcome to JSS3!

We are eager to have you join us in class!!

In today’s class, We will be discussing Whole Numbers. We hope you enjoy the class!

NUMBER BASE CONVERSIONS

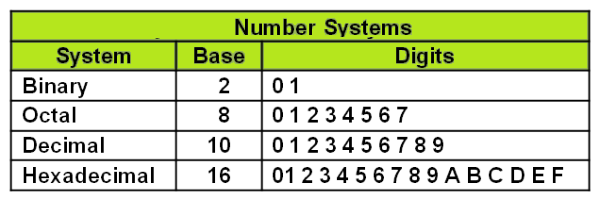
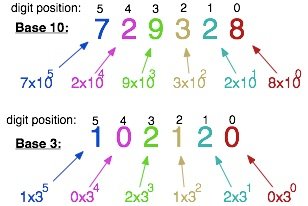
People count in twos, fives, twenties etc. Also, the days of the week can be counted in 24 hours. Generally, people count in tens. The digits 0,1,2,3,4,5,6,7,8,9 are used to represent numbers. The place value of the digits is shown in the number example: 395:- 3 Hundred, 9 Tens and 5 Units. i.e. 3X10² + 9 X 10¹ +5 X 10⁰.

Since the above number is based on the powers of tens it is called the base ten number system i.e. 300 + 90 + 5

Also 4075 = 4 Thousand 0 Hundred 7 Tens 5 Units i.e. 4 x 10³ + 0 X 10² + 7 X 10¹ + 5 X 10⁰ Other Number systems are sometimes used.

For Example: The base 8 system is based on the power of 8. For example: Expand 647₈, 26523₇, 1011012,

(a)    647₈  = 6 x 8² + 4 x 8¹ + 7 X 8⁰ =6 x 64 + 4 x 8 + 7 x 1

(b)    26523₇ =2 x 7⁴ + 6 x7³ + 5 x 7² + 2x 7¹ + 3 x 7⁰

(c)    101101₂= 1 x 2⁵ + 0 x 2⁴ + 1 x 2³ + 1 x 2² + 0 x2¹ + 1 x 2⁰

SELF EVALUATION

Expand The Following

1. 434₃
2. 101111₂

CONVERSION TO DENARY SCALE (BASE TEN)

When converting from other bases to base ten the number must be raised to the base and added.

Worked Examples:

Convert the following to base 10

(a)      17₈

(b)      11011₂

Solutions:

(a)      17₈ = 1 X 8¹ + 7 X 8⁰ = 1 X 8 + 7 X 1 = 8 + 7 = 15

(b)      11011₂ = 1 X 2⁴ + 1 X 2³ + 0 X 2² + 1 X 2¹ + 1 X 2⁰ = 1 X 16 + 1 X 8 + 0 X 4 + 1 X 2 + 1 X 1

= 16 + 8 + 0 + 2 + 1 = 27

SELF EVALUATION

Convert The Following To Base Ten:

(a)      10100₂

(b)      2120₃

CONVERSION FROM BASE TEN TO OTHER BASES

To change a number from base ten to another base

1. Divide the base ten number by the new base number.
2. Continue dividing until zero is reached
3. Write down the remainder each time
4. Start at the last remainder and read upwards to get the answer.

Worked Examples:

1. Convert 68₁₀ to base 6
2. Covert 129₁₀ to base 2

Solutions:

$$\begin{gathered} 1. \\ 6 | 68 \\ 6 | 11 R 2 \\ 6 | 1 R 5 \\ 0 | 1 \\ = {152}_6 \end{gathered}$$

$$\begin{gathered} 2. \\ 2 | 129 \\ 2 | 64 R 1 \\ 2 | 32 R 0 \\ 2 | 16 R 0 \\ 2 | 8 R 0 \\ 2 | 4 R 0 \\ 2 | 2 R 0 \\ 2 | 1 R 0 \\ 2 | 0 R 1 \\ = {10000001}_2 \end{gathered}$$

SELF EVALUATION

1. Convert 569₁₀ to base 8
2. Convert 100₁₀ to base 2

GENERAL  SELF EVALUATION

Convert the following to base seven

1. 405₁₀
2. 876₁₀

Evaluate the following

3.      5 – 3 + 4

We have come to the end of this class. We do hope you enjoyed the class?

Should you have any further question, feel free to ask in the comment section below and trust us to respond as soon as possible.

In our next class, we will be talking about Whole Numbers II. We are eager to meet you there.