Electric Field

Back to: PHYSICS SS3

 

Welcome to class! 

In today’s class, we will be talking about the electric field. Enjoy the class!

Electric Field

Concept of electric fields

The electric field is defined as any region where a charge experiences a force of electric origin. Electric lines of force are imaginary lines drawn in such a way that the direction at any point of the tangent is the same as the direction of the field at the same point.

Coulomb’s law

The electric force between two point charges, q₁ and q₂ separated by a distance r is directly proportional to the product of the charges and inversely proportional to the square of the distance between the charges

Mathematical expression

Worked examples

(1) Find the force of electrostatic repulsion between two particles of equal charges of 1.6 x 10^-19C, if the distance them r is 5.3 x 10^-11m.

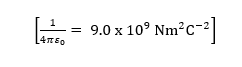
Solution

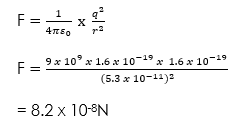
Where F = force of repulsion

q = a charge

 

(2) Calculate the electrostatic force of attraction between two charges, if the distance apart is 5 x 10¹⁰m given the Q and q are 1.65 x 10^-10C and 1.55 x 10^-10C respectively. (K = 9 x 10⁹m/f).

Solution

Given parameters:

Q = 1.65 x 10^-10C

q = 1.55 x 10^-10C

r = 5 x 10¹⁰m

K = 9 x 10⁹m/f

F = Unknown

Electric Field, Electric Field Intensity and Electric Potential

Electric field intensity

Electric field strength or Intensity (E) at a point, is defined as the magnitude of the force per unit positive charge at that point. This field is represented by electric line force which shows the direction of the field and their intensity or strength. For a point charge, q, the field at a distance, r is given by:

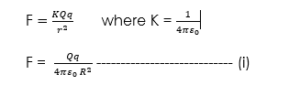
Since electric field strength or intensity is the force per unit coulomb

Worked example

(1) Two similar but opposite point charges –q and +q each of magnitude 5.0 x 10^-8C are separated by a distance of 8.0cm in a vacuum as shown in the diagram below.

Calculate the magnitude and direction of the resultant electric field intensity E at point P.

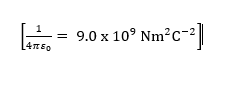
Solution

At P the vector due to  -q is directed towards the left and its magnitude is:

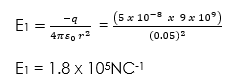
The vector due to +q is also directed towards the left and its magnitude is:

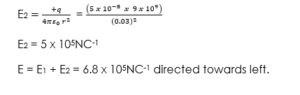
Electric potential

Electric potential, V is inversely proportional to the distance r from the charge Q which produce the field and given by:

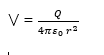
(1) A small positive charge q of +2 x 10-8C is at O, find the potential at B if the distance from O to B is 20cm.

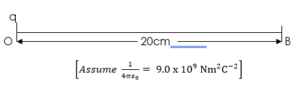
Solution

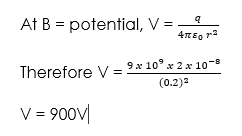
Presentation

1. Introduce the lesson by giving them definitions of Electric field.
2. Explain all the definitions by giving examples on each of them.
3. Pick out the keywords in the definitions and explain to them.
4. Ask them to defined Electric Potential by using their own words and correct them if necessary.
5. Define Electric field intensity
6. Solve questions that are related to this topic from Past Question.

Closure/summary

Teacher summarizes the lesson.

General evaluation

1. Calculate the electric field intensity at a point 15cm from a point of 10F.

Assignment

 1. Explain the terms:

(i) Electric field

(ii) Electric intensity

Write down the expression for the electric intensity at a distance r metre from a point charge Q Coulomb.

 2. A small object carrying a charge of -5 x 10^-9 C experiences a downward force of 10N when placed at a certain point in an electric field.

(i) What is the electric intensity at that point?

(ii) What would be the acting on an electron placed at that point? (Charge on an electron = 1.6 x 10^-19C)

 

In our next class, we will be talking more about Electric Field. We hope you enjoyed the class.

Should you have any further question, feel free to ask in the comment section below and trust us to respond as soon as possible.

For more class notes, homework help, exam practice, download our App HERE

Join ClassNotes.ng Telegram Community for exclusive content and support HERE