Wave Nature of Matter

Welcome to class!

In today’s class, we will be talking about the wave nature of matter. Enjoy the class!

Wave nature of matter means that matter behaves like a wave and exhibits the characteristic or properties of waves. Wave nature of matter implies that matter undergoes reflection, interference, refraction, diffraction and other properties of waves.

Examples of matter (Particles) that have wave nature

Electron
X – rays
Photons
Light energy

Albert Einstein in his explanation of the photoelectric effect assumed that the energy of light beam travels through space in packets or bundle called photons.

Louis de Broglie, a French scientist suggested that light energy behaves like a wave because it exhibits reflection, refraction and diffraction, which are features of waves. He later stated that the wavelength of the wave along with particles was given as:

ʎ = h /ƿ

ʎ = h/mv (ƿ = mv).

Where ʎ is the wavelength, h is Planck constant = 6.63 x 10⁻³⁴ Js,

v is velocity and m is mass of electron = 9.1×10 ⁻³¹ kg.

He said that electron has wave particles, x – rays.

Compton, with experiment, showed that the conservation of momentum and energy were obeyed when x –rays were incident on an electron.

Drag’s law of diffraction of x-rays

Drag law of diffraction of x- rays state that when a monochromatic x-ray impinging upon the atom in a crystal lattice, each atom acts as a source of scattered radiation of the same wavelength, the crystal act as a series of parallel reflecting planes.

Therefore, x –rays would be reflected by ordinary laws of reflection and the planes will reflect x – rays at all angles.

Duality of matter

Wave duality of matter simply refers to as the behaviour of matter, like a wave and like a particle. The wave-particle duality of matter is a general nature of matter. Matter has the properties of a wave and the properties of particles.

The formula for solving a problem in wave-particle of matter

Since matter has the properties of wave and particle, the Einstein energy equation for particle and light are combined to obtain the formula for solving a problem in wave-particle nature of matter. Thus:

Particle energy equation is E = mc² … equation 1, and

Wave/ light energy equation is E = hf … equation 2.

Let us substitute equation 1 for equation 2. Therefore,

E = mc² = hf

mc² = hf.

Recall that f =

Note that c = v. then

mc² = hf

mc² = h x

mc = .

Where c = v is the velocity, h is Planck constant, λ is wavelength and m is mass.

Worked examples

(1) What is the wavelength of an electron moving at the speed of 10⁶ m/s if the mass of the electron is (1 x 10³⁰ kg, e = 1.6 x 10 ̄ ¹⁹C, c = 8.0 x 10⁸ m/s, h = 6.6 x 10 ̄ ³⁴ Js)

(b) What is the energy of an electron with a wavelength of 10⁻¹² m. calculate the potential difference of the electron before it could be accelerated to acquire that velocity?

e = 1.6 x 10 ̄ ¹⁹C, Me = 9.1 x 10 ̄ ³¹kg, h = 6.6 x 10 ̄ ³⁴ Js,

Solution

Extract data are given in the question:

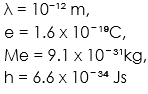
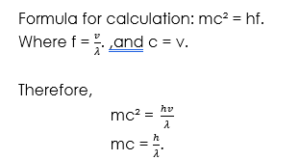
Note, we are to calculate the potential difference of the electron. The formula that contains the potential difference is the electron volt formula which is eV. Recall that electron volt is defined as the energy of electron when the electron is under the influence of a p.d of 1volt.

Therefore, eV = K. E

eV = ½mv².

From the question, v is not given. So we must first calculate v using the formula, mc² = hf, before we calculate the potential difference.

Therefore,

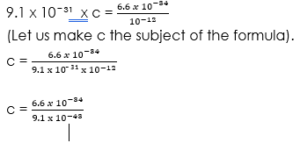
c = 0.7253 x 10⁹ m/s.

Now that we have calculated the velocity of the electron, we will now be able to calculate the potential difference using the formula,

eV = K.E

eV = ½mv².

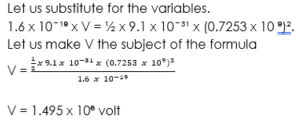
Uncertainty principle

Heisenberg’s uncertainty principle states that there is always uncertainty in the determination or measurement of the position and momentum of an electron at the same time. There must be a deviation in the actual value compared with the true value.

In other words, he states that it is practically impossible to obtain an accurate result in determining or measuring the position and momentum of an electron at the same time.

Formulae

He assumed that if the change in distance and velocity is the uncertainty of a distance and velocity o fan atomic scale. Then,

∆x. ∆v > h / m.

Where m is mass of the particle. Therefore

∆p . ∆x > h (m∆v = ∆p) or

∆E . ∆x ≥ h,

∆p. ∆x ≥ h,

∆. ∆t ≥ h

Where p is momentum; ∆p is change in momentum, x is distance; ∆x is change in distance, E is energy; ∆E is change in energy, t is time; ∆t is change in energy.

General evaluation

State the Heisenberg’s uncertainty principle. Mention two phenomena that can only be explained in terms of the particulate nature of light

Assignment

The uncertainty in determining the duration during which an electron remains in a particular energy level before returning to the ground state is 2.0 x 10 ⁻⁹s. Calculate the uncertainty in determining its energy at that level. (π = 22/7, h = 6.6 x 10 ̄ ³⁴ Js).

In our next class, we will be talking more about Radioactivity. We hope you enjoyed the class.

Should you have any further question, feel free to ask in the comment section below and trust us to respond as soon as possible.

For more class notes, homework help, exam practice, download our App HERE

Join ClassNotes.ng Telegram Community for exclusive content and support HERE

Wave Nature of Matter