Back to: PHYSICS SS3
Welcome to class!
In today’s class, we will be talking about the alternating current circuit. Enjoy the class!
Alternating Current Circuit
INTRODUCTION
Simple A.C circuits
An alternating current a.c. is a current which varies periodically. The electric circuit in which an alternating current flow is called an alternating circuit.
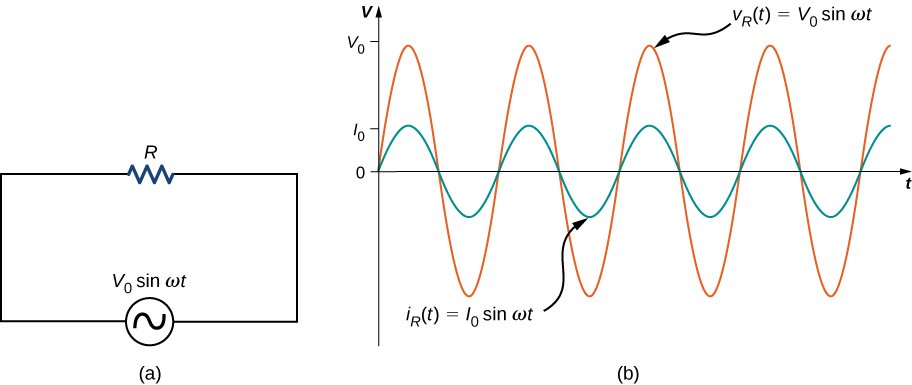
Figure (b) shows above v – t relation
The e.m.f., E varies sinusoidally with time in a rotating coil which is given by:
E =E0 sin 2πf
E = E0 sin
Where E, E0 = Em is the instantaneous and maximum (peak) values of E or its amplitude respectively.
or 2πf = phase angle
For figure (b) l – t relation
If an alternating current l varied sinusoidally, it could be represented by the equation:
I = Im sin 2πf
I = Im sin
Where
I = instantaneous current at time t
Im = maximum (peak) value of current or its amplitude
or (2πf) = angular frequency of the current
f = frequency
= phase angle which is the state of a periodically varying system at a particular time.
Note:
The phase difference between the voltage and the current through an RLC series circuit is represented by the equation:
The phase of an A.C. quantity
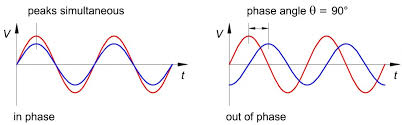
The phase of an A. C. quantity represents the fraction of the time period of that alternating quantity that has elapsed since the current last passed through the zero position of reference. The phase is also expressed in terms of angle in radians. For example phase at A is T/4 second or π/2 radians. In electricity, we are more concerned with the phase difference rather than an absolute phase of an alternating quantity. The phase difference between quantities indicates the lag or lead of an alternating quantity with respect to the other.
A leading quantity is a quantity which reaches maximum (or zero) value earlier as compared to the other quantity while lagging alternating quantity is one which reaches its zero or maximum value later than the other quantity. In figure two alternating quantities are shown quantity A leads B by an angle ϕ. Hence their equations are
IA = Imax sin wt and IB = Imax sin (ωt + ϕ)
Peak and root mean square (r.m.s) of a.c.
The peak or amplitude of the current I0 is the maximum numerical value of the current.
The root mean square (r.m.s) value of an alternating current is that direct current which produces the same heating effect per second in a given resistor.
P = I2R
For an a.c. circuit, the instantaneous power is given by
P = IV (instantaneous values)
Ir.m.s = = Ieff.
Where I0 is the maximum steady current.
Similarly Vr.m.s = = Veff.
Where r.m.s. is the root mean square and V0, the peak value or the maximum steady voltage.
The mean or average value of an alternating quantity
The mean value or average value (Iav) of an alternating current is equal to the steady current which transfers across any circuit the same charge as is transferred by the alternating current during the same time.
In the case of sinusoidal or symmetrical alternating current, the average value over the complete cycle is zero. Hence in these cases, the average value is obtained by integrating the instantaneous values of alternating quantity over half cycle only. The alternating currents average value is given by
Iav=2Imaxπ or Iav=0.637Imax
Representation of AC and voltage by rotating vectors
A phasor is a vector which rotates about the origin with angular speed ω, as shown in the figure given below:
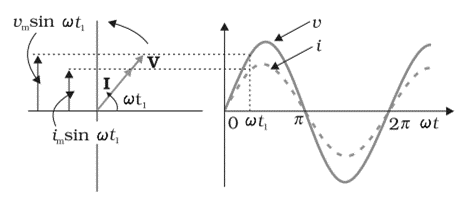
The vertical components of phasors V and I represent the sinusoidally varying quantities v and i. The magnitudes of phasors I and V represent the amplitudes or the peak values Vm and im of these oscillating quantities. The projection of voltage and current phasors on the vertical axis, i.e., Vm sinωt and im sinωt respectively represent the value of current and voltage at that instant.
Worked examples
(1) When the R.M.S. voltage of a square of electricity supply is given 240V, calculate the peak value of the supply.
Solution
(2) Calculate the instantaneous value of the current if in a circuit it has r.m.s. value of 15.0A when its phase angle is 30°
(3) In an a.c. circuit the peak value of the potential difference is 180V. What is the instantaneous p.d. when it is reached 1/8th of a circle?
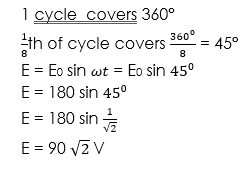
A.C. circuit containing resistance only (Resistive circuit)
AC circuit containing resistance only is a circuit which consists of a resistor as shown in the figure below
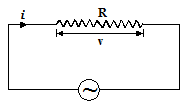
A.C circuit containing resistance only
Since the circuit is non-inductive, it is easy to apply Ohm’s law
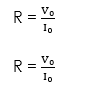
Maximum current flows in this circuit
Phase relationship
V = V0 sin
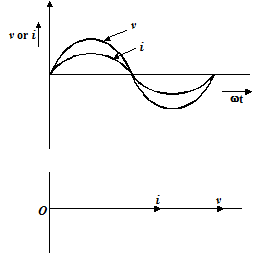
The current is in phase with the applied voltage. The phase difference is Z0.
Worked examples
(1) A 240 V is connected with a resistor of 20 Ω in an A.C circuit. Find:
(i) the current in the circuit
(ii) The phase angle and draw the phase diagram.
Solution
(ii) Since there is no other circuit in the element, the angle is 0°.
General evaluation
- Define alternating current.
Assignment
(1) (a) Explain what is meant by the r.m.s value of an alternating current. If the alternating current is represented by I = Im sinx, state what the symbols I, I0, and represent.
(b) Calculate the instantaneous value of such a current, if in a circuit it has r.m.s. value of 15.0A when its phase angle is 30°.
(2) Explain the meaning of Peak value of an alternating current. If the peak value of such a current is 15A, calculate its root mean square value.
In our next class, we will be talking more about Alternating Current Circuit. We hope you enjoyed the class.
Should you have any further question, feel free to ask in the comment section below and trust us to respond as soon as possible.
School Owner? Looking for ready-made content and tools to save time and grow easily? Book a free demo session nowGet more class notes, videos, homework help, exam practice on Android [DOWNLOAD]
Get more class notes, videos, homework help, exam practice on iPhone [DOWNLOAD]