Back to: PHYSICS SS3
Welcome to class!
In today’s class, we will be talking more about radioactivity. Enjoy the class!
Radioactivity II
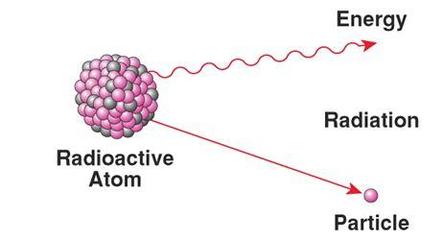
Radioactive decay
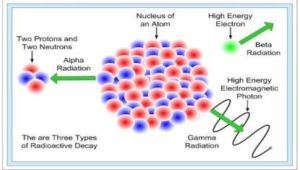
There are three types of radioactive decays in nature:
(i) α-decay –a helium nucleus (42He) is emitted
(ii) β-decay – where electrons or positrons (particles with the same mass as electrons, but with a charge exactly opposite to that of an electron) are emitted;
(iii) γ-decay – high energy (hundreds of keV or more) photons are emitted.
Law of radioactive decay
When a radioactive material undergoes α, β or γ-decay, the number of nuclei undergoing the decay, per unit time, is proportional to the total number of nuclei in the sample material. So,
If N = total number of nuclei in the sample and ΔN = number of nuclei that undergo decay in time Δt then,
ΔN/ Δt ∝ N
Or, ΔN/ Δt = λN … (1)
Where λ = radioactive decay constant or disintegration constant. Now, the change in the number of nuclei in the sample is, dN = – ΔN in time Δt. Hence, the rate of change of N (in the limit Δt → 0) is,
dN/dt = – λN
Or, dN/N = – λ dt
Now, integrating both the sides of the above equation, we get,
NN0∫ dN/N = λ tt0∫ dt … (2)
Or, ln N – ln N0 = – λ (t – t0) … (3)
Where, N0 is the number of radioactive nuclei in the sample at some arbitrary time t0 and N is the number of radioactive nuclei at any subsequent time t. Next, we set t0 = 0 and rearrange the above equation (3) to get,
ln (N/N0) = – λt
Or, N(t) = N0e– λt … (4)
Equation (4) is the Law of Radioactive Decay.
The decay rate
In radioactivity calculations, we are more interested in the decay rate R (= – dN/dt) than in N itself. This rate gives us the number of nuclei decaying per unit time. Even if we don’t know the number of nuclei in the sample, by simply measuring the number of emissions of α, β or γ particles in 10 or 20 seconds, we can calculate the decay rate. Let’s say that we consider a time interval dt and get a decay count ΔN (= –dN). The decay rate is now defined as,
R = – dN/dt
Differentiating equation (4) on both sides, we get,
R = λ N0 e−λt
Or, R = R0e−λt … (5)
Where, R0 is the radioactive decay rate at the time t = 0, and R is the rate at any subsequent time t. Equation (5) is the alternative form of the Law of Radioactive Decay. Now we can rewrite equation (1) as follows,
R = λN … (6)
Where R and the number of radioactive nuclei that have not yet undergone decay must be evaluated at the same instant.
Half-life and mean life
The total decay rate of a sample is also known as the activity of the sample. The SI unit for measurement of activity is ‘becquerel’ and is defined as,
1 becquerel = 1 Bq = 1 decay per second
An older unit, the curie, is still in common use:
1 curie = 1 Ci = 3.7 × 1010 Bq (decays per second)
There are two ways to measure the time for which a radionuclide can last.
- Half-life T1/2 – the time at which both R and N are reduced to half of their initial values
- Mean life τ – the time at which both R and N have been reduced to, e-1 of their initial values.
Calculating half-life
Let’s find the relation between T1/2 and the disintegration constant λ. For this, let’s input the following values in equation (5),
R = (1/2)R0 and t = T1/2
So, we get T1/2 = (ln2)/ λ
Or, T1/2 = 0.693/ λ … (7)
Calculating mean life
Next, let’s find the relation between the mean life τ and the disintegration constant λ. For this, let’s consider equation (5),
- The number of nuclei which decay in the time interval: ‘t’ to ‘t + Δt’ is: R(t)Δt = (λN0e–λt Δt).
- Each of them has lived for time ‘t’.
- Hence, the total life of all these nuclei is tλN0e–λt Δt
Hence, to obtain the mean life, we integrate this expression over all the times from 0 to ∞ and divide by the total number of nuclei at t = 0 (which is N0).
τ = (λN0 0∞∫ te–λtdt)/N0
= λ0∞∫ te–λtdt
On solving this integral, we get
τ = 1/λ
Therefore, we can summaries the observations as follows:
t½ = (ln2)/λ = τ ln 2 … (8)
Worked examples
(1) An element source has a decay constant of 1.3 x 10-11s-1. Calculate the half-life of the element.
Solution
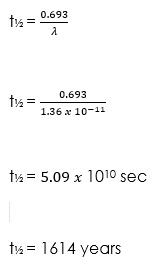
(2) The original quantity of a radioisotope is given as 100 millicuries, if the quantity remaining after 6days is 75 millicuries, calculate the
(i) Decay constant
(ii) Half-life of the radio-isotope.
Solution
(i) Parameters given
N0 = 100 millicuries (mci),
N = 75 mci and
t = 6 days
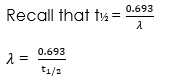
The decay constant can also be expressed as:
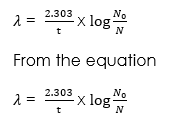
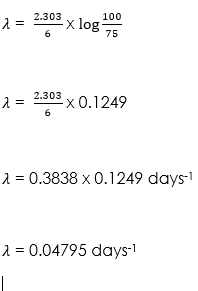
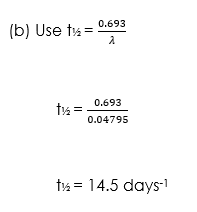
General evaluation
- State the law of Radioactivity Decay.
Assignment
- Calculate the half-life of radio-isotope which has a decay constant of 0.000456 per day.
We hope you enjoyed the class.
Should you have any further question, feel free to ask in the comment section below and trust us to respond as soon as possible.
