Back to: PHYSICS SS3
Welcome to class!
In today’s class, we will be talking about electric measurement. Enjoy the class!
Electric Measurement
Resistivity
The resistivity of a material is a fundamental property of a material that quantifies how strongly a given material opposes the flow of current. The resistivity of a material is highly dependent on temperature.
Therefore, at a constant temperature resistance varies directly as the length and inversely as the cross-section area of the conductor;
R α L/A
R= (A constant x L/A)
Or simply, AR/L= constant
The constant is called the resistivity of the material;
Resistivity = (cross section area A x resistance R) / length L.
Resistivity is measured in ohm-metre (Ωm).
Electrical conductivity
Electrical conductivity is defined as the reciprocal of resistivity. It is denoted by K and measured in Ω-1m-1 or (Ωm)-1.
Thus,
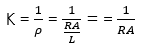
Worked examples
(1) A wire of resistance 3.5Ω has a length of 0.5m and cross-section area 8.2 x 10-8m2. Determine its resistivity.
Solution
Resistivity = AR/L = (8.2 x 10-8m2 x 3.5Ω)/0.5m
= 5.74 x 10-7Ωm
(2) If a wire has a resistance of 1.32 Ω, a length of 110cm and an area of cross-sectional of 0.00415cm2, find the resistivity of the material of which it is made.
Solution
Given parameters:
L = 110cm = 1.1m
R = 1.32 Ω
A = 0.00415cm2 = 4.15 x 10-7m2
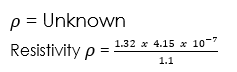
= 4.98 x 10-7Ωm
(3) A wire 40cm long and of diameter 0.06mm has a resistance of 1.5 Ω. What is the resistivity of the material of which it is made? [π = 3.142]
Solution
Given parameters:
L = 40mm = 0.4m
R = 1.5 Ω
d = 0.06mm = 6 x 10-4m2
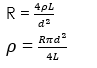
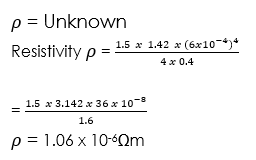
Galvanometer
It is an instrument used to detect small currents in a circuit.
The current required for full-scale deflection in the galvanometer is called full-scale deflection current and is denoted by Ig.
Current sensitivity of a galvanometer
It is defined as the deflection produced in the galvanometer when unit current flows through it.
Current sensitivity, Is = 
and its unit is rad A–1
Current sensitivity can be increased either by decreasing C i.e. restoring torque per unit twist or increasing B.
Voltage sensitivity of a galvanometer
It is defined as the deflection produced in the galvanometer when a unit voltage is applied across the two terminals of the galvanometer.
Voltage sensitivity, 
its unit is rad V–1
Ammeter
The ammeter is used to measure current in a circuit. An ammeter is always connected in series in the circuit as shown.
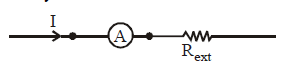
Conversion of a galvanometer into an ammeter
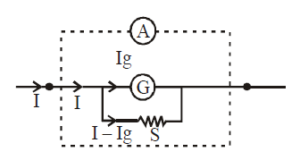
For this, we connect a small resistance S (called a shunt) in parallel with the galvanometer.
Mathematically, Ig × G = (I – Ig) S
Where I is the maximum current which ammeter can measure. G is the resistance of galvanometer and Ig is the current of full-scale deflection in the galvanometer. S is a shunt.
Resistance of the ammeter
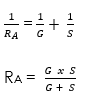
Since shunt is small resistance. Therefore the resistance of ammeter is very small.
The above arrangement is made so that when we connect an ammeter in series to measure current, it does not change the original current to a large extent. The change is in fact very small. Also since galvanometer is a sensitive device and cannot take large currents, this arrangement serves the purpose. Most of the current entering the ammeter pass through the shunt as current always prefer low resistance path.
An ideal ammeter is one which has zero resistance.
The range of ammeter can be increased but cannot be decreased below Ig.
Voltmeter
A voltmeter is used to measure the potential difference across a resistor. The voltmeter is always connected in parallel across a resistor.
Conversion of a galvanometer into a voltmeter
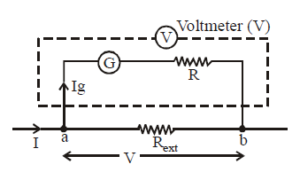
For this, we connect a large resistance R in series with the galvanometer.
The potential difference which has to be measured is across the external resistance i.e. across points a and b.
Let it be V. Then V = Ig (G + R)
where V is the maximum potential difference that the voltmeter can measure and R is the large resistance connected in series with the galvanometer
The resistance of the voltmeter will be RV = G + R
Since R is a large resistance. Therefore the resistance of voltmeter is very large.
An ideal voltmeter is one which has infinite resistance.
The range of voltmeter can be increased and decreased.
Note:- When ammeter/voltmeter is connected in the circuit, the current or voltage indicated by these is less than the actual values in their absence.
Physics Study Notes
Worked example
(1) A galvanometer of resistance 5 ohms gives a full-scale deflection when a current of 50mA flows through it. How will you convert it to an ammeter capable of measuring 2A?
Solution
To convert a galvanometer to an ammeter we connect a shunt of resistance RΩ in parallel with galvanometer to carry off any current in excess of 50mA or 0.05A.
Current flowing through the shunt = (2 – 0.05) = 1.95A
p.d. across shunt = (1.95 x R) volts
p.d. across galvanometer resistance = 0.05 x 5 volts
since p.d. across shunt = p.d. across the galvanometer resistance, we have
1.95 x R = 0.05 x 5
R = 0.05 * 5/1.95
R = 0.128Ω
Thus a small resistance of value 0.128Ω will convert the galvanometer to an ammeter reading up to 2A.
R = 0.128Ω
Thus a small resistance of value 0.128Ω will convert the galvanometer to an ammeter reading up to 2A.
Presentation
- Introduce the lesson by giving them definitions of Resistivity.
- Explain all the definitions by giving examples on each of them.
- Pick out the keywords in the definitions and explain to them.
- Ask them to Conductivity by using their own words and correct them if necessary.
- Define Galvanometer
- Solve simple calculation.
General evaluation
- What is an Ideal Voltmeter?
Assignment
- Calculate the length of constantan wire of diameter 0.6mm and resistivity 1.1 x 10-6 Ωm required to construct a standard resistor of resistance 35V.
- A galvanometer of resistance 50Ω which gives a full-scale deflection for 1mA is to be adapted to measure currents of up to 5A.
- Calculate the resistance of the resistor required
- If this resistor is made of a material of cross-sectional area 0.0004cm2 and resistivity of 0.000002 Ωcm, calculate its length.
In our next class, we will be talking about Magnetic Field. We hope you enjoyed the class.
Should you have any further question, feel free to ask in the comment section below and trust us to respond as soon as possible.
School Owner? Looking for ready-made content and tools to save time and grow easily? Book a free demo session nowGet more class notes, videos, homework help, exam practice on Android [DOWNLOAD]
Get more class notes, videos, homework help, exam practice on iPhone [DOWNLOAD]