Back to: PHYSICS SS3
Welcome to class!
In today’s class, we will be talking about the gravitational field and law. Enjoy the class!
Gravitational Field and Law
Concept of fields
Any region in the space under the influence of some physical agency such as gravitational, electricity and magnetic is known as a field. Examples of fields include the gravitational, magnetic, electric and nuclear fields.
Gravitational field
A gravitational field is any region or space around a mass in which the gravitational force of the mass is felt. The gravitational field was first studied or observed on the planet by a scientist called Tycho Brahe. He states three laws called Kepler’s laws.
Gravitational forces between two masses
The gravitational force exists between two objects on the earth surface at a distance from each other. The pull of gravity acts on the mass of all sizes. An example is the car slopes down to the attraction of the earth as it is pulled.
Newton’s law of universal gravitation
Newton’s law of universal gravitation states that the force of attraction between two given particles is inversely proportional to the square of their distance apart.
From Newton’s law, it follows that the force of attraction, F, between two particles of masses, m and M respectively at a distance r apart, is given by:
Therefore: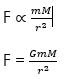 
Where G is the proportional constant known as gravitational constant.
Relationship between the force of gravity, mass and acceleration due to gravity
Force (F) = mass (m) x acceleration due to gravity (g)
Therefore: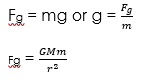 
But
Where M is the mass of the earth, G the gravitational constant (S.I unit is Nm2/kg2), m the mass of the object and r the Earth’s radius
Gravitational potential and escape velocity
-
Gravitational potential
The potential due to the gravitational field of the earth is defined as numerically equal to the work done in taking a unit mass from infinity to that point. On the surface of the earth, we can show that the gravitational potential (V) is given by:
-
Escape velocity
Escape velocity (Ve) as the minimum velocity required for an object (e.g. satellite or rocket) to just escape or leave the gravitational influence or field of an astronomical body (e.g. the earth) permanently.
Mathematical expression
Work done = Kinetic energy
Kepler’s law
Kepler’s laws of planetary motion describe the orbits of objects about the sun. The laws can be stated as follows:
Law 1: State that the planets describe eclipse of the sun as one focus.
Law 2: The line joining the sun and the planets sweep out equal areas in equal time
Law 3: The Square of the periods of revolution of the planets are proportional to the cube to their mean distance from the sun.
Worked examples
(1) Calculate the gravitational force of attraction between two protons in a chemical compound. Take the mass of a proton as 1.67 x 10-27kg and the distance between the protons in the chemical compound as 10-10m.
Solution
Given parameters:
r = 10-10m
m and M = 1.67 x 10-27kg
G = 6.67 x 10-11kg (Constant)
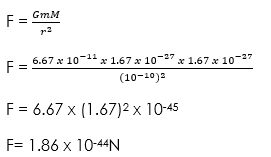
(2) Calculate the escape velocity of a satellite from the earth’s gravitational field. (g = 9.8m/s2, radius of earth = 6.4 x 106m)
Solution
Given parameters:
General evaluation
- What do you understand by field, a gravitational field?
Assignment
- State Newton’s law of universal gravitational. Write down the expression for the gravitational force between two masses. Explain the meaning of each term in your expression.
- Calculate the force or attraction between two small objects of mass 10kg and 50kg respectively which are 10cm apart. Take G as 6.67 x 10-11Nm2kg-2.
- State Kepler’s laws pertaining to the motion of the solar system.
We hope you enjoyed the class.
Should you have any further question, feel free to ask in the comment section below and trust us to respond as soon as possible.
School Owner? Looking for ready-made content and tools to save time and grow easily? Book a free demo session nowGet more class notes, videos, homework help, exam practice on Android [DOWNLOAD]
Get more class notes, videos, homework help, exam practice on iPhone [DOWNLOAD]
Formica for escape velocity?
This was helpful